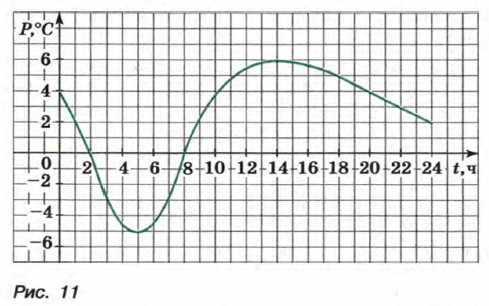
Свойства функций

На рисунке 11 изображен график зависимости температуры воздуха Р (°С) от времени суток t (ч). Мы видим, что в 2 ч и в 8 ч температура равнялась нулю, от 0 до 2 ч и от 8 до 24 ч она была выше нуля, а от 2 до 8 ч — ниже нуля. Из графика ясно также, что в течение первых пяти часов температура понижалась, затем в промежутке от 5 до 14 ч она повышалась, а потом опять понижалась.

С помощью графика мы выяснили некоторые свойства функции Р = ƒ(t), где t — время суток в часах, а Р — температура воздуха в градусах Цельсия.

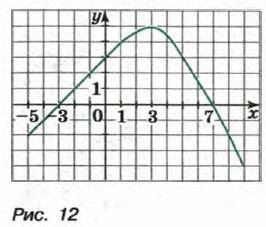
Рассмотрим теперь свойства функции у = ƒ(x), где -5 ≤ х ≤ 9, график которой изображен на рисунке 12. Выясним сначала, при каких значениях х функция обращается в нуль, принимает положительные и отрицательные значения.

Найдем абсциссы точек пересечения графика с осью х. Получим х = — 3 и х = 7. Значит, функция принимает значение, равное нулю, при х = — 3 и х — 7. Значения аргумента, при которых функция обращается в нуль, называют нулями функции, т. е. числа -3 и 7 — нули рассматриваемой функции. Нули функции разбивают ее область определения — промежуток [-5; 9] на три промежутка: [-5; -3), (-3; 7) и (7; 9]. Для значений х из промежутка (-3; 7) точки графика расположены выше оси х, а для значений х из промежутков [-5; -3) и (7; 9] — ниже оси х. Значит, в промежутке (—3; 7) функция принимает положительные значения, а в каждом из промежутков [-5; -3) и (7; 9] — отрицательные.

Промежутки, в которых функция сохраняет знак, называют промежутками знакопостоянства.

Выясним теперь, как изменяются (увеличиваются или уменьшаются) значения данной функции с изменением х от -5 до 9.

Из графика видно, что с возрастанием х от -5 до 3 значения у увеличиваются, а с возрастанием х от 3 до 9 значения у уменьшаются. Говорят, что в промежутке [-5; 3] функция у = ƒ(x) является возрастающей, а в промежутке [3; 9] эта функция является убывающей.

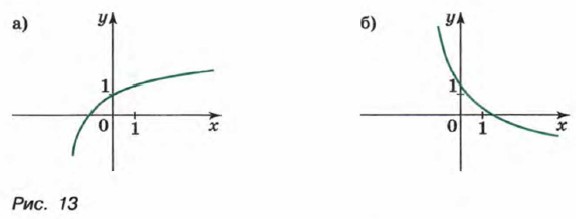
Определение. Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Иными словами, функцию у = ƒ(x) называют возрастающей в некотором промежутке, если для любых х₁ и х₂ из этого промежутка, таких, что х₂ > х₁, выполняется неравенство ƒ(x₂) > ƒ(x₁); функцию у = ƒ(x) называют убывающей в некотором промежутке, если для любых х₁ и х₂ из этого промежутка, таких, что х₂ > х₁, выполняется неравенство ƒ(x₂) < ƒ(x₁).

Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией.

На рисунке 13 изображены графики возрастающей функции и убывающей функции.

Выясним, какими свойствами обладают некоторые изученные ранее функции.

Продолжение >>>