|
|
|
|
|
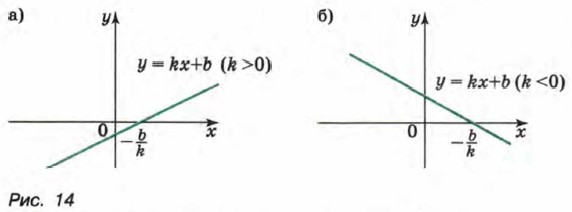
§ 1. Функции и их свойства Свойства функций (продолжение)Пример 1. Рассмотрим свойства функции у = kx + b, где k ≠ 0 (рис. 14).
1. Функция обращается в нуль при Действительно, решив уравнение kx + b = 0, найдем, что у = 0 при 2. При k > 0 функция принимает отрицательные значения в промежутке Решив неравенства kx + b < 0 и kx + b > 0, найдем, что если k > 0, то у < 0 при При k < 0 функция принимает отрицательные значения в промежутке Убедиться в этом можно, решив неравенства kx + b < 0 и kx + b > 0 при условии, что k < 0. 3. При k > 0 функция у = kx + b является возрастающей, а при k < 0 — убывающей. Докажем это. Пусть х1 и х2 — произвольные значения аргумента, причем х2 > х1. Обозначим через у1 и у2 соответствующие им значения функции: у1 = kx1 + b и у2 = kx2 + b. Рассмотрим разность у2 - у1: у2 - у1 = (kx2 + b) - (kx1 + b) = kx2 - kx1 = k(x2 - x1). Множитель х2 - x1 положителен, так как х2 > x1 Поэтому знак произведения k(x2 - x1) определяется знаком коэффициента k. Если k > 0, то k(x2 - x1) > 0 и у2 > y1. Значит, при k > 0 функция у = kx + b является возрастающей. Если k < 0, то k(x2 - x1) < 0 и у2 < y1. Значит, при k < 0 функция у = kx + b является убывающей. Пример 2. Рассмотрим свойства функции
1. Функция нулей не имеет. Это следует из того, что дробь 2. Функция Действительно, если k > 0, то дробь Функция Обоснование аналогично изложенному для случая k > 0. 3. При k > 0 функция Доказательство этого свойства проводится аналогично тому, как это было сделано для линейной функции. Заметим, что, хотя функция
|
|
|



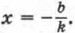
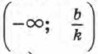 и положительные значения в промежутке
и положительные значения в промежутке 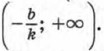
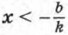 и у > 0 при
и у > 0 при 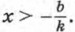
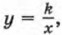 где k ≠ 0 (рис. 15).
где k ≠ 0 (рис. 15).
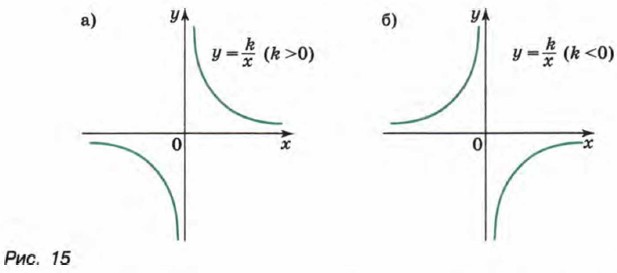
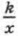 при любом значении аргумента не обращается в нуль (по условию k ≠ 0).
при любом значении аргумента не обращается в нуль (по условию k ≠ 0).
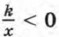 при х < 0 и
при х < 0 и 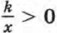 при х > 0.
при х > 0.