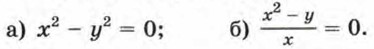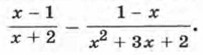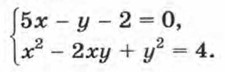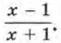|
|
|
|
|
§ 8. Неравенства с двумя переменными и их системы Неравенства с двумя переменными (ответы)485. Изобразите на координатной плоскости множество точек, за- — даваемое неравенством ах + by > с, если: а) а = 0, b = 1, с = 3; б) а = 1, b = 0, с = 3. 486. Изобразите на координатной плоскости множество точек, задаваемое неравенством: а) х ≥ 3; б) у ≤ -1; в) 1 ≤ х ≤ 4; г) -3 < у < 3. 487. Изобразите на координатной плоскости множество решений неравенства:
488. Изобразите на координатной плоскости множество решений неравенства: а) ху > 12; б) xу < 4. 489. Какое множество точек задается неравенством: а) х2 + у2 - бx - 4у + 13 ≤ 0; б) х2 - 4х - у + 5 ≥ 0? 490. Задайте неравенством с двумя переменными: а) круг с центром в точке (2; 0) и радиусом, равным 3;
491. Опишите неравенством множество точек координатной плоскости, расположенных: а) выше параболы у = х2 - 9;
492. Изобразите на координатной плоскости множество решений неравенства: а) ху ≥ 0; б) ху < 0. Упражнения для повторения493. Постройте график уравнения:
494. Представьте в виде рациональной дроби:
495. Решите систему уравнений
Ответы489. а) Точка (3; 2); б) множество точек, принадлежащих параболе у = (х - 2)2 + 1, и точек, расположенных ниже ее. 490. а) (х - 2)2 + у2 ≤ 9; б) х2 + (у - 4)2 > 4. 492. а) Множеством решений является объединение первой и третьей четвертей координатной плоскости, включая оси координат; б) множеством решений является объединение второй и четвертой четвертей координатной плоскости, кроме осей координат. 494. 495. (1; 3), (0; -2).
|
|
|