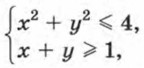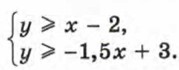|
|
|
|
|
§ 8. Неравенства с двумя переменными и их системы Системы неравенств с двумя переменнымиРассмотрим систему неравенств с двумя переменными
Пара чисел (1; 2) значений переменных х и у является решением как первого, так и второго неравенства системы, т. е. является общим решением неравенств этой системы. Такую пару чисел называют решением системы неравенств с двумя переменными. Множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в нее неравенств. На координатной плоскости множество решений системы неравенств изображается множеством точек, представляющих собой общую часть множеств, задаваемых неравенствами, входящими в систему. Рассмотрим примеры. Пример 1. Выясним, какое множество точек задает на координатной плоскости система неравенств
Итак, множеством точек, которое задает система неравенств
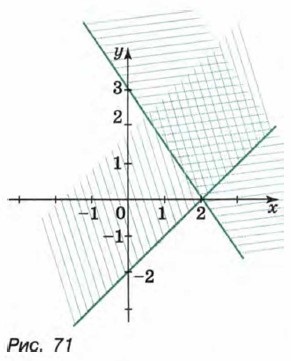
является сегмент, показанный на рисунке 70 двойной штриховкой. Остановимся подробнее на примерах систем, состоящих из двух линейных неравенств. Пример 2. Изобразим на координатной плоскости множество решений системы
|
|
|



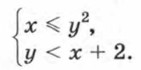
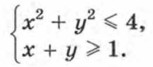
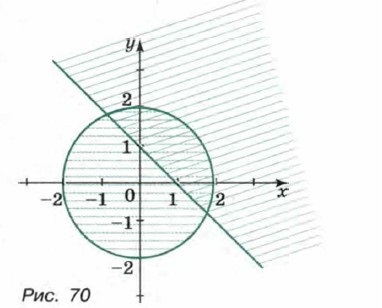
 Первое неравенство системы задает на координатной плоскости круг с центром в начале координат и радиусом, равным 2. На рисунке 70 это множество точек показано горизонтальной штриховкой. Второе неравенство задает полуплоскость, которая показана на рисунке 70 наклонной штриховкой. Множество решений системы изображено двойной штриховкой.
Первое неравенство системы задает на координатной плоскости круг с центром в начале координат и радиусом, равным 2. На рисунке 70 это множество точек показано горизонтальной штриховкой. Второе неравенство задает полуплоскость, которая показана на рисунке 70 наклонной штриховкой. Множество решений системы изображено двойной штриховкой.