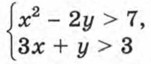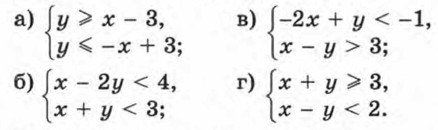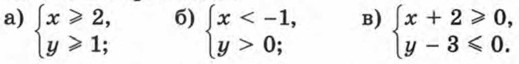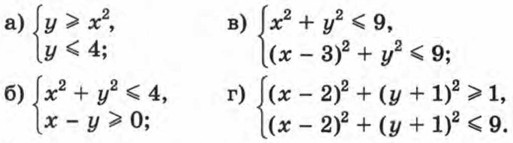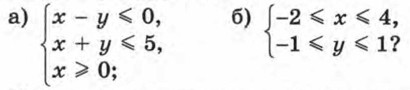|
|
|
|
|
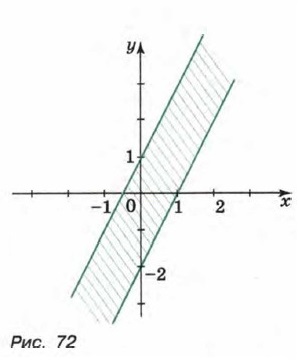
§ 8. Неравенства с двумя переменными и их системы Системы неравенств с двумя переменными (продолжение)Пример 3. Выясним, какое множество точек задает на координатной плоскости система неравенств
Упражнения496. Является ли решением системы неравенств
пара чисел: а) (4; 2); б) (-5; 1); в) (-2; -1); г) (6; -5)? 497. Покажите штриховкой на координатной плоскости множество ~ решений системы неравенств:
498. Изобразите на координатной плоскости множество решений системы неравенств:
499. Задайте системой неравенств: а) первую координатную четверть (включая оси координат);
500. Изобразите на координатной плоскости множество решений "" системы:
501. Какую фигуру задает множество решений системы неравенств:
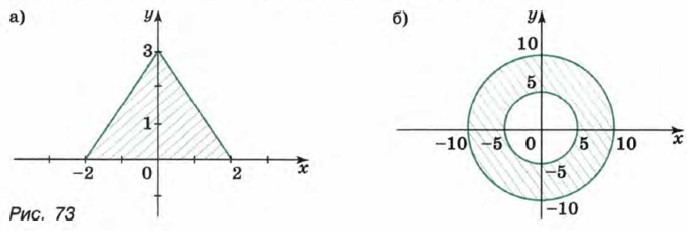
Найдите площадь каждой фигуры. 502. Задайте системой неравенств: а) треугольник, изображенный на рисунке 73, а;
503. Одна из сторон острого угла проходит через точки (0; 0) и (3; 3), а другая — через точки (0; -2) и (3; -2). Задайте этот угол системой неравенств.
|
|
|



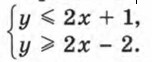
 Множество точек, задаваемое первым неравенством, — полуплоскость, расположенная ниже прямой у = 2х + 1. Множество точек, задаваемое вторым неравенством, — полуплоскость, расположенная выше прямой у = 2х - 2. Так как угловые коэффициенты прямых y = 2x + 1 и у = 2х- 2 равны, то прямые параллельны. Следовательно, пересечением указанных полуплоскостей является полоса, изображенная на рисунке 72.
Множество точек, задаваемое первым неравенством, — полуплоскость, расположенная ниже прямой у = 2х + 1. Множество точек, задаваемое вторым неравенством, — полуплоскость, расположенная выше прямой у = 2х - 2. Так как угловые коэффициенты прямых y = 2x + 1 и у = 2х- 2 равны, то прямые параллельны. Следовательно, пересечением указанных полуплоскостей является полоса, изображенная на рисунке 72.