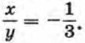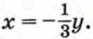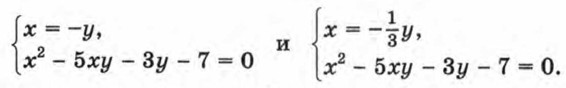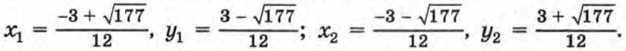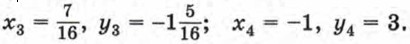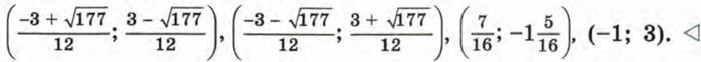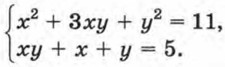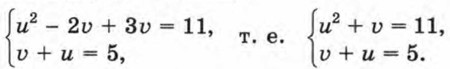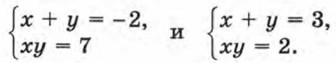|
|
|
|
|
Для тех, кто хочет знать больше Некоторые приемы решения систем уравнений второй степени с двумя переменными (продолжение)Пример 3. Решим систему
Левая часть первого уравнения системы — однородный многочлен, т. е. многочлен, каждый член которого имеет одну и ту же степень. Разделим обе части первого уравнения на у2, предполагая, что у * 0. Получим квадратное относительно
является равносильной исходной системе. Обозначив Отсюда х = -у или Таким образом, решение исходной системы можно свести к решению совокупности двух систем:
Решив первую систему, найдем, что
Решив вторую систему, найдем, что
Решения исходной системы:
Пример 4. Решим систему
Уравнения в этой системе содержат сумму переменных х + у, произведение ху и сумму квадратов х2 + у2. Если в этой системе заменить х на у, а у на х, то получим ту же систему. Такие системы называют симметрическими системами. Их удобно решать, вводя новые переменные. Пусть х + у = u, ху = υ. Тогда х2 + у2 = (х + у)2 - 2ху = u2 - 2υ. В результате получим систему
Решив эту систему способом подстановки, найдем, что u1 = -2, υ1 = 7, u2 = 3, υ2 = 2. Выполнив обратную замену, получим совокупность систем
Первая система не имеет решений. Вторая имеет решения (1; 2) и (2; 1). Решения исходной системы: (1; 2), (2; 1).
|
|
|



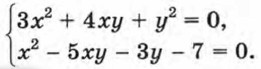
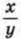 уравнение
уравнение 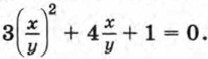 При этом мы потеряем решение (0; 0) первого уравнения системы. Но так как пара (0; 0) не является решением второго уравнения, то система
При этом мы потеряем решение (0; 0) первого уравнения системы. Но так как пара (0; 0) не является решением второго уравнения, то система
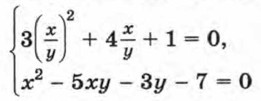
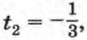 т. е.
т. е. 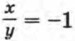 или
или