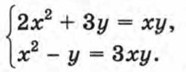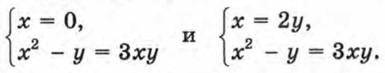|
|
|
|
|
Для тех, кто хочет знать больше Некоторые приемы решения систем уравнений второй степени с двумя переменнымиВы познакомились со способом решения систем уравнений с двумя переменными, в которых одно уравнение первой степени, а другое — второй степени. Такие системы решаются способом подстановки. Покажем на примерах некоторые приемы решения систем уравнений, в которых оба уравнения второй степени. Пример 1. Решим систему уравнений
Система уравнений перепишется в виде
Произведение (х - 3у)(х + 3у - 1) равно нулю тогда и только тогда, когда х - 3у = 0 или х + 3у - 1 = 0. Решениями исходной системы являются те пары значений переменных х и у, которые удовлетворяют системе уравнений
или системе уравнений
Поэтому множеством решений исходной системы является объединение множеств решений систем (1) и (2). Говорят, что данная система равносильна совокупности систем уравнений (1) и (2). Решим первую систему. Выполнив подстановку х = 3у, получим квадратное уравнение 6у2 + у - 7 = 0, корнями которого являются числа Решим систему (2). Выполнив подстановку х= -3у + 1, получим квадратное уравнение (-3у + 1)2 - у(-3у + 1) + у - 7 = 0, которое после упрощения примет вид 2у2 - у - 1 = 0. Отсюда Значит, система (2) имеет решения (2,5; -0,5), (-2; 1). Решения исходной системы: Таким образом, мы решили исходную систему уравнений, заменив ее совокупностью двух систем. Пример 2. Решим систему уравнений
Первая система имеет единственное решение: (0; 0), вторая система имеет два решения: (0; 0) и (-1; -0,5). Решения исходной системы: (0; 0), (-1; -0,5).
|
|
|



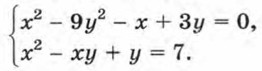
 В этой системе многочлен, записанный в левой части первого уравнения, можно разложить на линейные множители:
В этой системе многочлен, записанный в левой части первого уравнения, можно разложить на линейные множители:
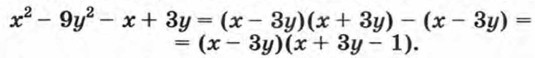
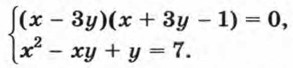


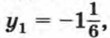 у2 = 1. Подставив их значения в первое уравнение, найдем, что
у2 = 1. Подставив их значения в первое уравнение, найдем, что 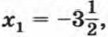 х2 = 3. Значит, система (1) имеет решения
х2 = 3. Значит, система (1) имеет решения 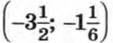 и (3; 1).
и (3; 1).
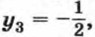 у4 = 1. Подставив эти значения в первое уравнение системы (2), найдем, что х3 = 2,5, х4 = -2.
у4 = 1. Подставив эти значения в первое уравнение системы (2), найдем, что х3 = 2,5, х4 = -2.
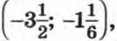 (3; 1), (2,5; -0,5), (-2; 1).
(3; 1), (2,5; -0,5), (-2; 1).