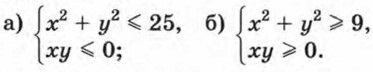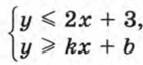Дополнительные упражнения к параграфу 8

550. Изобразите на координатной плоскости множество решений неравенства:

а) у - 2х > 2; б) х + у < -1.

551. Изобразите на координатной плоскости множество точек, задаваемое неравенством:

а) (x - З)² + (у + 3)² ≤ 4; б) у ≤ х² - 5x + 6.

552. Где на координатной плоскости расположены точки, у которых:

а) абсцисса больше ординаты;
б) ордината больше абсциссы?

553. Какое множество точек координатной плоскости задается неравенством:

а) х² + у² - 4х - 8у ≤ 0; б) х² - 6х 4- у + 4 > 0?

554. Изобразите на координатной плоскости множество решений неравенства:

а) у ≥ |х|; б) у ≤ |х- 2|.

555. Какое множество точек задает на координатной плоскости неравенство:

а) (х - 1)(у - 1) ≥ 0; б) х² - у² > 0?

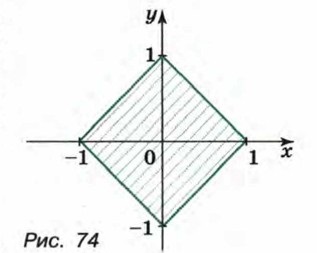
556. Докажите, что множество решений неравенства |x| + |y| ≤ 1 задается фигурой, изображенной на рисунке 74.

557. Изобразите на координатной плоскости множество решений системы неравенств:

558. Укажите какие-нибудь значения k и b, при которых система неравенств

задает на координатной плоскости:

а) полосу; б) угол.

559. Каким множеством точек изображается множество решений неравенства:

а) у(х² + у² - 1) ≥ 0; б) х(х² - у) ≤ 0?

Ответы

553. а) Круг с центром в точке (2; 4) и радиусом √20; б) множество точек координатной плоскости, расположенных выше параболы y = -(x - 3)² + 5.

555. а) Объединение двух прямых углов, образованных прямыми х = 1 и у = 1 и содержащих точки (2; 2) и (0; 0).

559. а) Объединение двух областей А и В, где А — верхняя полуплоскость (у ≥ 0), из которой исключен полукруг (х² + у² ≤ 1), В — полукруг, расположенный ниже оси х.