|
|
|
|
|
§ 9. Арифметическая прогрессия ПоследовательностиБудем выписывать в порядке возрастания положительные четные числа. Первое такое число равно 2, второе 4, третье 6, четвертое 8 и т. д. Получим последовательность 2; 4; 6; 8; ... . Ясно, что на пятом месте в этой последовательности будет число 10, на десятом — число 20, на сотом — число 200. Вообще для любого натурального числа n можно указать соответствующее ему положительное четное число; оно равно 2n. Рассмотрим еще одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:
Для любого натурального числа n мы можем указать соответствующую дробь, стоящую в этой последовательности на n-м месте; она равна Числа, образующие последовательность, называют членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена, например а1, а2, а3, а4 и т. д. (читают: «а первое, а второе, а третье, а четвертое» и т. д.). Вообще член последовательности с номером n, или, как говорят, n-й член последовательности, обозначают аn. Саму последовательность будем обозначать так: (аn). В рассмотренных примерах мы имели дело с последовательностями, содержащими бесконечно много членов. Такие последовательности называются бесконечными. Заметим, что последовательность может содержать конечное число членов. В таком случае ее называют конечной. Например, конечной является последовательность двузначных чисел 10; 11; 12; 13; ... ; 98; 99. Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером. Часто последовательность задают с помощью формулы n-го члена последовательности. Например, последовательность положительных четных чисел можно задать формулой аn = 2n, последовательность правильных дробей с числителем, равным 1, — формулой Пример 1. Пусть последовательность задана формулой уn = n2 - 3га. Подставляя вместо га натуральные числа 1, 2, 3, 4, 5 и т. д., получаем y1 = -2, у2 = -2, у3 = 0, у4 = 4, у5 = 10, ... . Рассматриваемая последовательность начинается так: -2; -2; 0; 4; 10; ... . Пример 2. Пусть последовательность задана формулой хn = (-1)n • 10. Все члены этой последовательности с нечетными номерами равны -10, а с четными номерами равны 10: х1 = -10, х2 = 10, х3 = -10, х4 = 10, ... . Получаем последовательность -10; 10; -10; 10; -10; ... . Пример 3. Формулой сn — 5 задается последовательность, все члены которой равны 5: 5; 5; 5; 5; 5; ... . Рассмотрим еще один способ задания последовательности. Он состоит в том, что указывают ее первый член или первые несколько членов и формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько). Такую формулу называют рекуррентной (от латинского слова recurro — возвращаться), а соответствующий способ задания последовательности — рекуррентным способом. Приведем пример задания последовательности рекуррентным способом. Пример 4. Пусть (un) — последовательность, в которой n1 = 1, u2 = 1, un + 1 = un + un - 1 при n > 2. Выпишем первые несколько ее членов: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... . Эта последовательность описана в работах итальянского математика Леонардо из Пизы, известного под именем Леонардо Фибоначчи (1180—1240). Члены этой последовательности называют числами Фибоначчи.
|
|
|



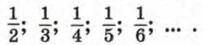
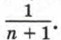 Так, на шестом месте должна стоять дробь
Так, на шестом месте должна стоять дробь 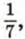 на тридцатом — дробь
на тридцатом — дробь 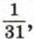 на тысячном — дробь
на тысячном — дробь 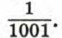
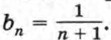 Приведем другие примеры.
Приведем другие примеры.