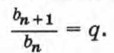Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

2; 2²; 2³; 2⁴; 2⁵; 2⁶; ... .

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность (b_n) — геометрическая прогрессия, если для любого натурального n выполняются условия

b_n ≠ 0 и b_{n +1} = b_n • q,

где q — некоторое число.

Обозначим, например, через (b_n) последовательность натуральных степеней числа 2. В этом случае для любого натурального n верно равенство b_{n + 1} = b_n • 2, здесь q = 2.

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство

Число q называют знаменателем геометрической прогрессии. Ясно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Приведем примеры.

Если b₁ = 1 и q = 0,1, то получим геометрическую прогрессию

1; 0,1; 0,01; 0,001; 0,0001; ... .

Условиями b₁ = -5 и q = 2 задается геометрическая прогрессия

-5; -10; -20; -40; -80; ... .

Если b₁ = 2 и q = -3, то имеем прогрессию

2; -б; 18; -54; 162; ... .

Если b₁ = 8 и q = 1, то получим геометрическую прогрессию

8; 8; 8; 8; 8; ... .

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:

b₂ = b₁q,
b₃ = b₂q = (b₁q)q = b₁q²,
b₄ = b₃q = (b₁q²)q = b₁q³,
b₅ = b₄q = (b₁q³)q = b₁q⁴.

Точно так же находим, что b₆ = b₁q⁵, b7 = b₁q⁶ и т. д. Вообще, чтобы найти b_n, мы должны b₁ умножить на q^{n - 1}, т. е.

b_n = q^{n - 1}

Мы получили формулу n-го члена геометрической прогрессии.

Приведем примеры решения задач с использованием этой формулы.

Продолжение >>>