|
|
|
|
|
§ 10. Геометрическая прогрессия Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии (продолжение)Пример 1. В геометрической прогрессии b1 = 12,8 и Найдем b7.
Пример 2. Найдем восьмой член геометрической прогрессии (bn), если b1 = 162 и b3 = 18.
Решив уравнение
найдем, что
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи. Если
Если
Задача имеет два решения:
Пример 3. Вкладчик положил в банк 5000 р. на счет, по которому сумма вклада ежегодно возрастает на 8%. Какая сумма будет у него на счету через 6 лет?
Таким образом, мы имеем дело с геометрической прогрессией 5000, 5000 • 1,08, 5000 • 1,082, 5000 • 1,083, ... . Сумма, накопленная на счету у вкладчика, через 6 лет будет равна седьмому члену этой прогрессии, т. е. составит 5000 • 1,086. Выполнив вычисления, найдем, что 5000 • 1,086 ≈ 7934. (При выполнении вычислений удобно использовать калькулятор.) Значит, на счету у вкладчика через 6 лет окажется сумма, приближенно равная 7934 р. В рассмотренном примере нам приходилось вычислять один и тот же процент от величины, найденной на предыдущем шаге. В таких случаях говорят, что мы имеем дело со сложными процентами. Геометрическая прогрессия обладает следующим свойством:
bn = bn - 1g, bn + 1 = bnq. Так как все члены геометрической прогрессии отличны от нуля, то отсюда следует, что
Верно и обратное утверждение:
Докажите это самостоятельно. Заметим, что из равенства
|
|
|



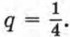
 По формуле n-го члена геометрической прогрессии
По формуле n-го члена геометрической прогрессии
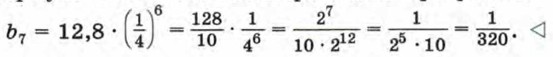
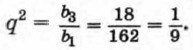
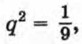
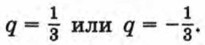
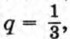 то
то
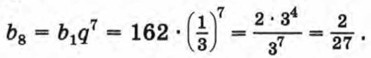
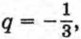 то
то
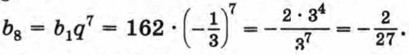
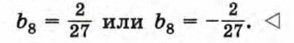

 Действительно, если последовательность (bn) является геометрической прогрессией, то
Действительно, если последовательность (bn) является геометрической прогрессией, то
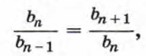
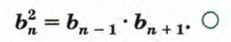
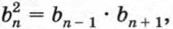 выражающего свойство геометрической прогрессии, следует, что
выражающего свойство геометрической прогрессии, следует, что 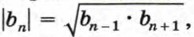 т. е. модуль любого члена геометрической прогрессии, начиная со второго, является средним геометрическим предыдущего и последующего членов.
т. е. модуль любого члена геометрической прогрессии, начиная со второго, является средним геометрическим предыдущего и последующего членов.