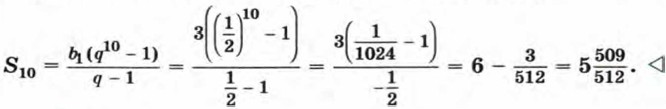Формула суммы первых n членов геометрической прогрессии

Согласно легенде индийский принц решил наградить изобретателя шахмат и предложил ему самому выбрать награду. Изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и так далее до 64-й клетки. Каково же было удивление принца, когда он узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.

Действительно, число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:

S = 1 + 2 + 2² + 2³ + ... + 2⁶² + 2⁶³.

Умножим обе части записанного равенства на знаменатель прогрессии, получим

2S = 2 + 2² + 2³ + 2⁴ + ... + 2⁶³ + 2⁶⁴.

Вычтем почленно из второго равенства первое и проведем упрощения:

2S - S - (2 + 2² + ... + 2⁶³ + 2⁶⁴) - (1 + 2 + 2² + ... +2⁶³),
S = 2⁶⁴ - 1

Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Выведем теперь формулу суммы первых п членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

Пусть дана геометрическая прогрессия (b_n). Обозначим сумму первых п ее членов через S_n:

S_n = b₁ + b₂ + 6₃ + ... + b_{n - 1} + b_n. (1)

Умножим обе части этого равенства на q:

S_nq = b₁q + b₂q + b₃q + ... + b_{n - 1}q + b_nq.

Учитывая, что

b₁q = b₂, b₂q = b₃, b₃q = b₄, ... , b_{n - 1}q = b_n,

получим

S_ng = b₂ + b₃ + b₄ + ... + b_n + b_nq. (2)

Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:

S_nq - S_n = (b₂ + b₃ + ... + b_n + b_nq) - (6₁ + b₂ + ... + b_{n - 1} + b_n) = b_nq - b₁,
S_n(q - 1) = b_nq - 6₁.

Отсюда следует, что при q ≠ 1

Мы получили формулу суммы первых п членов геометрической прогрессии, в которой q ≠ 1. Если g = 1, то все члены прогрессии равны первому члену и S_n = nb₁.

При решении многих задач удобно пользоваться формулой суммы первых п членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо b_n выражение b₁q^{n - 1}. Получим

Пример 1. Найдем сумму первых десяти членов геометрической прогрессии (b_n), в которой b₁ = 3 и

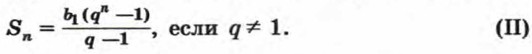
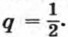
Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим

Продолжение >>>