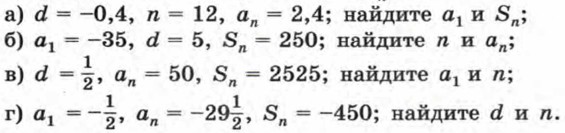|
|
|
|
|
Дополнительные упражнения к главе IV Дополнительные упражнения к параграфу 9 (продолжение)686. На одной стороне угла от вершины отложены двенадцать равных отрезков и через их концы (кроме вершины угла) проведены параллельные прямые, пересекающие другую сторону угла. Найдите сумму длин всех параллельных отрезков, заключенных между сторонами угла, если длина наименьшего из них равна 3 см. 687. В арифметической прогрессии (аn):
688. Найдите разность арифметической прогрессии (xn) и ее первый член, если х10 = 1 и S16 = 4. 689. Найдите сумму: а) всех двузначных чисел; б) всех трехзначных чисел. 690. Найдите сумму: а) всех натуральных четных чисел, не превосходящих 200;
691. Какова сумма натуральных чисел: а) меньших 100 и не кратных 3;
692. Найдите натуральное число, которое: а) в 5 раз меньше суммы предшествующих ему натуральных чисел;
693. Члены арифметической прогрессии 2; 5; ... с четными номерами заменили противоположными им числами. В результате получили последовательность (xn). Напишите формулу n-го члена этой последовательности и найдите сумму первых пятидесяти ее членов. 694.Упростите выражение:
895. Найдите: а) сумму всех положительных членов арифметической прогрессии 8,2; 7,4; ... ;
696. Найдите сумму первых сорока членов арифметической прогрессии, если S10 = 100 и S30 = 900. 697. Найдите пятидесятый член арифметической прогрессии, если: a) S20 = 1000, S40 = 10 000; б) S5 = 0,5, S15 = -81. 698. Запишите формулу суммы первых л членов последовательности (аn), если: a) аn = 2n + 1; б) аn = 3 - n. 699. Является ли последовательность (хn) арифметической прогрессией, если сумму первых л ее членов можно найти по формуле Sn = n2 - 8n? Найдите пятый член этой последовательности. 700. Является ли последовательность (хn) арифметической прогрессией, если сумма первых л ее членов может быть найдена по формуле:
|
|
|