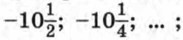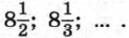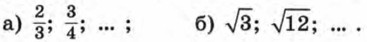|
|
|
|
|
Дополнительные упражнения к главе IV Дополнительные упражнения к параграфу 9670. Вычислите первые пять членов последовательности (сn), заданной формулой:
671. Задайте формулой n-го члена последовательность (аn), если: а) (аn) — последовательность натуральных чисел, кратных 5;
672. Вычислите первые несколько членов последовательности (уn), если:
673. Найдите члены арифметической прогрессии (аn), обозначенные буквами: a) a1; a2; -19; -11,5; a5; ... ; б) a1, -8,5, a3, -4,5, a5, a6, ... . 674. Периметр треугольника равен 24 см, причем длины его сторон образуют арифметическую прогрессию. Можно ли определить длину хотя бы одной из сторон? Какие целые значения могут принимать длины сторон треугольника, выраженные в сантиметрах? 675. Углы треугольника образуют арифметическую прогрессию. Докажите, что один из них равен 60°. 676. Последовательность (аn) — арифметическая прогрессия. Является ли арифметической прогрессией последовательность:
677. Последовательность (аn) — арифметическая прогрессия. Найдите:
678. Найдите номер члена арифметической прогрессии (аn): а) равного -2,94, если а1 = 1,26 и d = -0,3;
679. Дана арифметическая прогрессия (bn), у которой
680. Найдите: а) первый положительный член арифметической прогрессии б) первый отрицательный член арифметической прогрессии 681. Докажите, что если (уn) — арифметическая прогрессия, то: а) y2 + y7 = y4 + y5; б) yn - 5 + yn + 10 = yn + yn + 5, где n > 5. 682. Докажите, что если d — разность арифметической прогрессии, а xm и xn — ее члены, причем m ≠ n, то 683. Дана арифметическая прогрессия (аn). Найдите: a) d, если а20 = 1,7 и а37 = 0; б) а100, если a10 = 270 и d = -3. 684. Найдите сумму первых десяти членов арифметической прогрессии:
685. Найдите сумму, слагаемыми которой являются последовательные члены арифметической прогрессии: а) 2 + 6 + 10 + ... + 198; б) 95 + 85 + 75 + ... + (-155).
|
|
|



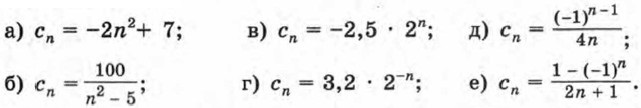
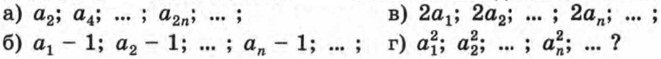
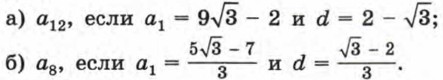
 и
и 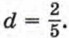 Является ли членом этой прогрессии число:
Является ли членом этой прогрессии число: