|
|
|
|
|
§ 2. Квадратный трехчлен Квадратный трехчлен и его корни (продолжение)Пример 3. Докажем, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат. Пусть одна сторона прямоугольника равна х см. Тогда другая сторона равна 10-х см, а площадь прямоугольника равна х(10 - х) см2. Раскрыв скобки в выражении х(10 - х), получим 10х - х2. Выражение -х2 + 10х представляет собой квадратный трехчлен, в котором а = — 1, b = 10, с = 0. Выделим квадрат двучлена:
Так как выражение (х - 5)2 при любом х ≠ 5 отрицательно, то сумма (х - 5)2 + 25 принимает наибольшее значение при х = 5. Значит, площадь будет наибольшей, когда одна из сторон прямоугольника равна 5 см. В этом случае другая сторона также равна 5 см, т. е. прямоугольник является квадратом. Упражнения55. Какие из чисел -2, -1, 0, 2, 3 являются корнями многочлена х3 - 3х2 - 4х + 12? 56. Найдите корни многочлена: а) х2 - 7х; б) 2х - 5; в) у3 - 4у; г) у4 - 16. 57. Имеет ли корни многочлен: а) х2 + 1; б) х3 - 27; в) -2у6 - 1; г) у4 + 3у2 + 7? 59. Найдите корни квадратного трехчлена:
60. Найдите корни квадратного трехчлена:
61. Имеет ли квадратный трехчлен корни и если имеет, то сколько:
62. Имеет ли квадратный трехчлен корни и если имеет, то сколько:
63. Сумма коэффициентов квадратного трехчлена равна нулю, а его свободный член в 4 раза больше старшего коэффициента. Найдите корни этого трехчлена. 64. Выделите квадрат двучлена из квадратного трехчлена:
65. Выделите квадрат двучлена из квадратного трехчлена:
66. Докажите, что при любом значении х квадратный трехчлен: а) х2 - 6х + 10 принимает положительное значение;
67. Даны квадратные трехчлены х2 - 6х + 11 и -х2 + 6х - 11. Докажите, что первый из них не принимает отрицательных значений, а второй — положительных. 68. При каком значении x трехчлен 2x2 - 4х + 6 принимает наименьшее значение? Найдите это значение. 69. Дан квадратный трехчлен 70. Докажите, что из всех прямоугольных треугольников с суммой катетов, равной 6 см, наибольшую площадь имеет равнобедренный треугольник. 71. С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 50 м/с, высота башни 20 м и t (с) — время полета стрелы, то расстояние h (м) стрелы от поверхности земли в момент времени t (с) можно найти по формуле h = -5t2 + 50t + 20 (приближенное значение ускорения свободного падения считается равным 10 м/с2). Какой наибольшей высоты достигнет стрела?
|
|
|



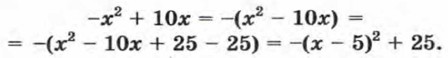
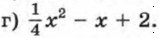
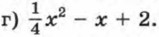
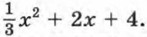 Выясните, при каком значении х он принимает наименьшее значение и чему равно это значение трехчлена.
Выясните, при каком значении х он принимает наименьшее значение и чему равно это значение трехчлена.