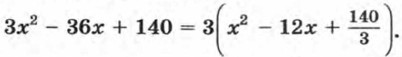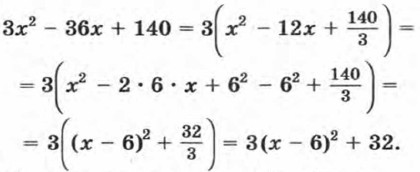|
|
|
|
|
§ 2. Квадратный трехчлен Квадратный трехчлен и его корниКаждое из выражений х5 - 2х4 + Зх3 - 7х + 2, 2у4 - у3 + 5у2 - 3у + 18, 7z6 - 6z4 + z2 - 2z + 3 является многочленом с одной переменной. Значение переменной, при котором многочлен обращается в нуль, называют корнем многочлена. Найдем, например, корни многочлена х3 - х. Для этого решим уравнение х3 - х = 0. Разложив левую часть уравнения на множители, получим х(х - 1)(х + 1) = 0, отсюда х1 = 0, х2 = 1, х3 = -1. Таким образом, числа 0, 1,-1 — корни многочлена х3 - х. Многочлен второй степени с одной переменной называют квадратным трехчленом.
Коэффициент а называют старшим коэффициентом, ас — свободным членом квадратного трехчлена. Примерами квадратных трехчленов являются многочлены 3х2 - 2х - 5, х2 + 7х - 8. В первом из них а = 3, b = -2, с = -5, во втором а = 1, 6 = 7, с = -8. К квадратным трехчленам относятся также и такие многочлены второй степени, у которых один из коэффициентов b либо с или даже оба равны нулю. Так, многочлен 7х2 - х считают квадратным трехчленом. У него а = 7, b = -1, с = 0. Для того чтобы найти корни квадратного трехчлена ах2 + bх + с, надо решить квадратное уравнение ах2 + bх + с = 0. Пример 1. Найдем корни квадратного трехчлена Зх2 - 2х - 5. Решим уравнение Зх2 - 2х - 5 = 0. Имеем
Значит, квадратный трехчлен 3х2 - 2х - 5 имеет два корня: Так как квадратный трехчлен ах2 + bх + с имеет те же корни, что и квадратное уравнение ах2 + bх + с = 0, то он может, как и квадратное уравнение, иметь два корня, один корень или не иметь корней. Это зависит от значения дискриминанта квадратного уравнения D = b2 - 4ac, который называют также дискриминантом квадратного трехчлена. Если D > 0, то квадратный трехчлен имеет два корня; если D = 0, то квадратный трехчлен имеет один корень; если D < О, то квадратный трехчлен не имеет корней. При решении задач иногда бывает удобно представить квадратный трехчлен ах2 + bх + с в виде а(х - m)2 + n, где m и n — некоторые числа. Такое преобразование называется выделением квадрата двучлена из квадратного трехчлена. Покажем на примере, как выполняется это преобразование. Пример 2. Выделим из трехчлена 3х2 - 3бх + 140 квадрат двучлена. Вынесем за скобки множитель 3:
Преобразуем выражение в скобках. Для этого представим 12х в виде произведения 2 • 6 • х, а затем прибавим и вычтем 62. Получим
Значит, 3х2 - 36х + 140 = 3(х - б)2 + 32. Рассмотрим задачу, при решении которой применяется выделение квадрата двучлена из квадратного трехчлена.
|
|
|



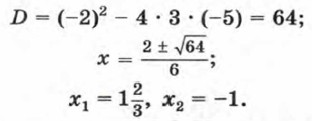
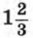 и -1.
и -1.