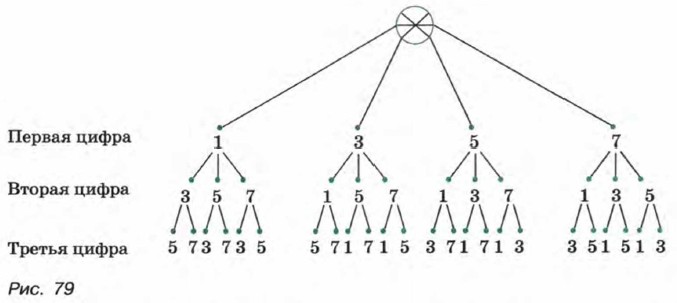
Примеры комбинаторных задач (продолжение)

Проведенный перебор вариантов проиллюстрирован на схеме, изображенной на рисунке 79. Такую схему называют деревом возможных вариантов.

Заметим, что ответ на вопрос, поставленный в примере 2, можно получить, не выписывая сами числа. Будем рассуждать так. Первую цифру можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4 • 3 • 2, т. е. 24. Мы нашли ответ на поставленный в примере 2 вопрос, используя так называемое комбинаторное правило умножения.

Сформулируем это правило в общем виде.

Пусть имеется n элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать n₁ способами, после чего второй элемент можно выбрать n₂ способами из оставшихся, затем третий элемент можно выбрать n₃ способами из оставшихся и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n₁ • n₂ • n₃ • ... • n_k.

Пример 3. Из города А в город В ведут две дороги, из города В в город С — три дороги, из города С до пристани — две дороги (рис. 80). Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из B в С тремя способами. Значит, имеются 2 • 3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2 • 3 • 2, т. е. 12, способов выбора туристами маршрута из города А к пристани.

Упражнения

714. В кафе предлагают два первых блюда: борщ, рассольник — и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из первого и второго блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов.

715. У Ирины пять подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?

716. Стадион имеет четыре входа: А, В, С и D. Укажите все возможные способы, какими посетитель может войти через один вход, а выйти через другой. Сколько таких способов?

717. Укажите все способы, какими можно разложить три яблока в две вазы (учтите при этом случаи, когда одна из ваз окажется пустой).

718. Составьте все возможные двузначные числа из указанных цифр, используя в записи числа каждую из них не более одного раза:

а) 1, 6, 8; б) 0, 3, 4.

719. Из цифр 1, 2, 3 составьте все возможные двузначные числа при условии, что:

а) цифры в числе не повторяются;
б) допускается повторение цифр в числе.

720. Используя цифры 0, 2, 4, 6, составьте все возможные трехзначные числа, в которых цифры не повторяются.

721. В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии. Сколько всего партий было сыграно?

<<< К началу Ответы >>>