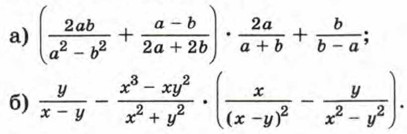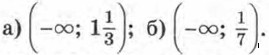Примеры комбинаторных задач (ответы)

722. В соревнованиях по футболу участвовало 12 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника. Сколько всего игр было сыграно?

723. При встрече 8 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

724. Учащиеся 9 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 учащихся?

725. На входной двери дома установлен домофон, на котором нанесены цифры 0, 1, 2, .... 8, 9. Каждая квартира получает код из двух цифр типа 0—2, 3—7, 7—3, 8—8 и т. п., позволяющий открывать входную дверь. Хватит ли кодов для всех квартир дома, если в доме 96 квартир?

726. Из села Дятлово в село Матвеевское ведут три дороги, а из села Матвеевское в село Першино — четыре дороги. Сколькими способами можно попасть из Дятлово в Першино через Матвеевское?

727. В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?

728. Петр решил пойти на новогодний карнавал в костюме мушкетера. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: пять видов брюк, шесть камзолов, три шляпы, две пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?

Упражнения для повторения

729.Упростите выражение:

730. Решите неравенство:

а) (2,5x + 3)(4х - 1) - 2,5х(4х + 2) < 3;
б) (1 - 4х)² - (8х - 1)(2х + 1) > 0.

731. Изобразите схематически график функции и укажите область ее значений:

а) у = х² + 15; б) у = (х - 16)²; в) у = -х² + 8.

Ответы

715. 10 вариантов.

716. 12 способов.

721. 36 партий.

722. 132 игры.

723. 28 рукопожатий.

724. 552 фотографии.

725. Хватит.

726. 12 способами.

727. 30 способами.

728. 180 костюмов.

729. а) 1; б) -1.

730.

<<< К началу