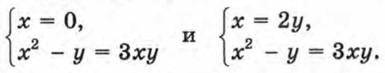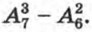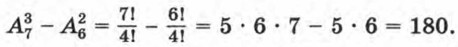Размещения (продолжение)

Рассмотрим примеры.

Пример 1. Учащиеся 2 класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?

Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо набором предметов, либо порядком их следования. Значит, в этом примере речь идет о размещениях из 9 элементов по 4. Имеем

Итак, мы нашли, что расписание можно составить 3024 способами.

Пример 2. Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0, 1, 2, 3, 4, 5, 6?

Если среди семи цифр нет нуля, то число трехзначных чисел (без повторения цифр), которые можно составить из этих цифр, равно числу размещений из 7 элементов по 3. Однако среди данных цифр есть цифра 0, с которой не может начинаться трехзначное число. Поэтому из размещений из 7 элементов по 3 надо исключить те, у которых первым элементом является цифра 0. Их число равно числу размещений из 6 элементов по 2.

Значит, искомое число трехзначных чисел равно

Получаем

Из данных цифр можно составить 180 трехзначных чисел (без повторения цифр).

Упражнения

754. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

755. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?

756. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?

757. Сколькими способами тренер может определить, кто из 12 спортсменок, готовых к участию в эстафете 4X100 м, побежит на первом, втором, третьем и четвертом этапах?

758. В круговой диаграмме круг разбит на 5 секторов. Секторы решили закрасить разными красками, взятыми из набора, содержащего 10 красок. Сколькими способами это можно сделать?

759. Сколькими способами 6 студентов, сдающих экзамен, могут — занять места в аудитории, в которой стоит 20 одноместных столов?

760. На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места:

а) 2 фотографии; б) 4 фотографии; в) 6 фотографий?

761. На плоскости отметили 5 точек. Их надо обозначить латинскими буквами. Сколькими способами это можно сделать (в латинском алфавите 26 букв)?

762. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр:

а) 1, 3, 5, 7, 9; б) 0, 2, 4, 6, 8?

763. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?

764. Сколько можно составить из цифр 1, 2, 3, 4, 5 (без их повторения) различных трехзначных чисел, которые являются:

а) четными; б) кратными 5?

<<< К началу Ответы >>>