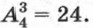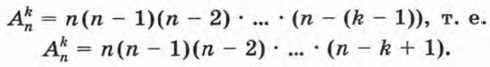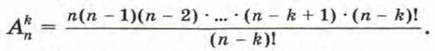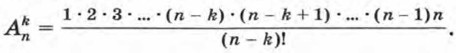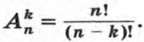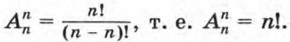|
|
|
|
|
§ 11. Элементы комбинаторики РазмещенияПусть имеется 4 шара и 3 пустые ячейки. Обозначим шары буквами a, b, с, d. В каждую ячейку можно поместить по одному шару из этого набора. Если мы поместим шар а в первую ячейку, шар b во вторую ячейку, а шар c в третью ячейку, то получим одну из возможных упорядоченных троек шаров:
Выбирая по-разному шары для первой, второй и третьей ячеек, будем получать различные упорядоченные тройки шаров, например:
Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три.
Таким образом, два размещения из n элементов по k считаются различными, если они различаются самими элементами или порядком их расположения. Число размещений из n элементов по k обозначают Составим из элементов a, b, с, d все размещения по три элемента. Выпишем сначала те размещения, которые начинаются с элемента а, затем те, которые начинаются с элемента b, с элемента с, с элемента d. В результате получим: abc, abd, acb, acd, adb, adc,
Из составленной таблицы видно, что Число размещений из четырех элементов по три можно найти, не выписывая самих размещений. Будем рассуждать так. Первый элемент можно выбрать четырьмя способами, так как им может быть любой из четырех элементов. Для каждого выбранного первого элемента можно тремя способами выбрать из трех оставшихся второй элемент. Наконец, для каждых первых двух элементов можно двумя способами выбрать из двух оставшихся третий элемент. В результате получаем, что С помощью тех же рассуждений нетрудно подсчитать, сколько можно составить размещений из п элементов по k при k < n. Первый элемент можно выбрать п способами. Так как после этого остается n — 1 элементов, то для каждого выбора первого элемента можно n — 1 способами выбрать второй элемент. Далее, для каждого выбора первых двух элементов можно n — 2 способами выбрать третий элемент (из n - 2 оставшихся) и т. д. Наконец, для каждого выбора первых k — 1 элементов можно n — (k — 1) способами выбрать k-й элемент (из n — (k - 1) оставшихся). Значит,
Умножим и разделим правую часть этого равенства на (n — k)!:
Заменив (n - k)! произведением 1 • 2 • 3 • ... • (n — k) и расположив множители в порядке возрастания, получим
В числителе дроби записано произведение всех натуральных чисел от 1 до n. Это произведение равно n!. Значит,
Мы получили формулу для вычисления числа размещений из n элементов по k при k < n. Формула верна и в том случае, когда k = n, если условиться считать по определению, что 0! = 1. Заметим, что размещения из n элементов по n отличаются друг от друга только порядком элементов, т. е. представляют собой перестановки из n элементов. В этом случае по формуле числа размещений получаем, что
Мы пришли к уже известной формуле числа перестановок.
|
|
|



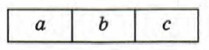

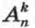 (читается: «А из n по k»).
(читается: «А из n по k»).
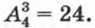
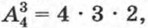 т. е.
т. е.