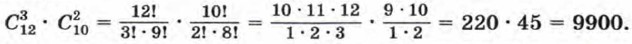|
|
|
|
|
§ 11. Элементы комбинаторики Сочетания (продолжение)Пример 2. В классе учатся 12 мальчиков и 10 девочек. Для уборки территории около школы требуется выделить трех мальчиков и двух девочек. Сколькими способами это можно сделать?
Имеем
Значит, выбор учащихся для уборки территории можно сделать 9900 способами. Упражнения768. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде? 769. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора? 770. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг? 771. На плоскости отмечено 8 точек, никакие три из которых не лежат на одной прямой. Сколько прямых можно провести через эти точки? 772. Из лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если: а) заведующий лабораторией должен ехать в командировку;
773. На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если: а) словарь нужен ему обязательно;
774. Бригада, занимающаяся ремонтом школы, состоит из 12 маляров и 5 плотников. Из них для ремонта физкультурного зала надо выделить 4 маляров и 2 плотников. Сколькими способами можно это сделать? 775. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала? В задачах 776—782 рассматриваются различные комбинации элементов (перестановки, размещения, сочетания). 776. Сколько среди всех перестановок букв слова «высота» таких, которые: а) начинаются с буквы «в»;
777. Пять мальчиков и четыре девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела между двумя мальчиками. Сколькими способами они могут это сделать? 778. Из 12 солдат, в число которых входят Иванов и Петров, надо отправить в наряд трех человек. Сколькими способами это можно сделать, если: а) Иванов и Петров должны пойти в наряд обязательно;
779. В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира: а) команду из четырех человек;
780. Номер машины в некотором городе составляют из двух различных букв, взятых из набора М, Н, К, Т, С, и трех различных цифр. Сколько машин можно обеспечить такими номерами? 781. Максим подсчитал, что существует 378 способов выбора из их класса двух дежурных. Сколько учащихся в этом классе? 782. Из группы туристов четырех дежурных можно выбрать в 13 раз большим числом способов, чем двух дежурных. Сколько туристов в группе?
|
|
|



 Выбрать трех мальчиков из 12 можно
Выбрать трех мальчиков из 12 можно 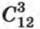 способами, а двух девочек из 10 можно выбрать
способами, а двух девочек из 10 можно выбрать 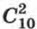 способами. Так как при каждом выборе мальчиков можно
способами. Так как при каждом выборе мальчиков можно 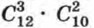 способами.
способами.