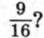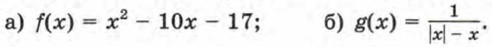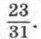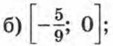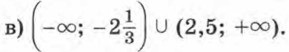Относительная частота случайного события (ответы)

791. Согласно некоторым исследованиям по изучению вероятности появления различных букв в художественных классических текстах, относительная частота появления буквы «в» равна 0,038, буквы «м» — 0,026.

Ниже приведен отрывок из поэмы А. С. Пушкина «Руслан и Людмила»:

У лукоморья дуб зеленый;
Златая цепь на дубе том:
И днем и ночью кот ученый
Все ходит по цепи кругом;
Идет направо — песнь заводит,
Налево — сказку говорит.
Там чудеса: там леший бродит,
Русалка на ветвях сидит.

Найдите относительную частоту появления в этом тексте:

а) буквы «в»; б) буквы «м».

Сравните полученные результаты с вышеперечисленными данными.

792. Проделайте дома такой опыт: подбросьте 50 раз монету достоинством 1 р. и подсчитайте, сколько раз выпадет орел. Запишите результаты в тетрадь. В классе подсчитайте, сколько всеми учениками было проведено опытов и каково общее число выпадений орла. Вычислите относительную частоту выпадения орла при бросании монеты.

793. Отмечая число попаданий в цель в каждой серии из 50 выстрелов, которые производил стрелок, получили такие данные:

38, 40, 42, 40, 39, 42, 43, 45, 40.

Какова относительная частота попаданий в цель этим стрелком в каждой серии выстрелов? Какое предположение о вероятности попадания в цель для этого стрелка можно сделать?

794. Готовясь к соревнованиям, баскетболист совершил 16 штрафных бросков, при этом мяч 9 раз попал в корзину. Можно ли утверждать, что для данного баскетболиста вероятность попадания мяча в корзину при выбрасывании штрафных очков равна

795. Многократная проверка показала, что всхожесть семян огурцов определенного сорта равна 0,9. Посадили 85 семян этого сорта. Какое предположение можно сделать о числе проросших семян?

Упражнения для повторения

796.Найдите область определения и область значений функции:

797. Решите неравенство:

а) 4х - 5х² < 0; б) 9х² ≤ -5х; в) 6х² - х - 35 > 0.

Ответы

787. 0,012.

788.

794. Нельзя.

795. ≈77.

796. а) (-∞; +∞); [-42; +∞); б) (-∞; 0); (0; +∞).

797. а) (-∞; 0) U (0,8; +∞);

<<< К началу