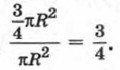|
|
|
|
|
§ 12. Начальные сведения из теории вероятностей Вероятность равновозможных событий (продолжение)Пример 3. Из 16 собранных велосипедов 4 оказались с дефектами. Какова вероятность того, что 2 выбранных наугад велосипеда будут без дефектов?
Пример 4. Группа туристов, в которой 7 юношей и 4 девушки, выбирает по жребию четырех дежурных. Какова вероятность того, что будут выбраны 2 юноши и 2 девушки?
Пусть А — событие, при котором выбраны 2 юноши и 2 девушки. Выбрать 2 юношей из 7 можно
Введем теперь понятия достоверного и невозможного событий. Событие, которое при проведении некоторого опыта или наблюдения происходит всегда, называют достоверным событием. Пусть С — событие, состоящее в том, что при бросании игрального кубика выпадет менее 7 очков. Это событие является достоверным. Каждый из исходов 1, 2, 3, 4, 5, 6 является благоприятным для события С. Значит, вероятность наступления события С равна:
Вообще вероятность достоверного события равна 1. Событие, которое не может произойти ни при каком исходе опыта или наблюдения, называют невозможным событием. Обозначим буквой F событие, означающее, что при бросании игрального кубика выпадает 7 очков. Очевидно, что это событие произойти не может. Число благоприятных для него исходов равно
Вообще вероятность невозможного события равна 0. Пусть некоторое испытание имеет n равновозможных исходов, из которых m исходов благоприятны для события А. Тогда
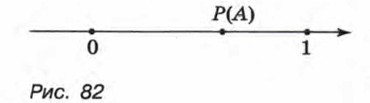
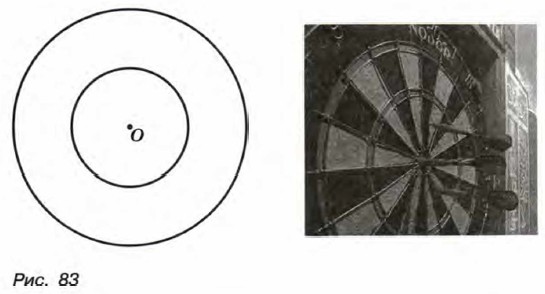
Это можно проиллюстрировать с Р(А) помощью вероятностной шкалы (рис. 82). Точкой 0 изображается вероятность невозможного события, а точкой 1 — вероятность достоверного события. Если событие А не является ни невозможным, ни достоверным событием, то Р(А) изображается точкой, расположенной между 0 и 1. Чем меньше вероятность наступления события А, тем ближе к 0 расположена точка Р{А). Чем больше вероятность наступления события А, тем ближе к 1 расположена точка Р(А). Вероятность случайного события иногда удается найти, используя геометрические соображения. Рассмотрим такой пример. Участники игры поочередно бросают в мишень дротики (специальные стрелы). Мишень представляет собой круг, в котором выделены малый круг и кольцевая зона, причем радиус малого круга вдвое меньше радиуса большого круга (рис. 83).
Найдем вероятность того, что при попадании дротика в мишень точка попадания окажется в кольцевой зоне. Будем считать, что попадание дротика в любую точку мишени равновозможно и вероятность попадания дротика в какую-либо область прямо пропорциональна площади этой области. Пусть радиус большого круга, представляющего собой мишень, равен R, тогда радиус центрального круга равен
|
|
|



 Пусть А — событие, при котором 2 выбранных велосипеда окажутся без дефектов. Любой выбор двух велосипедов из 16 является равновозможным исходом. Значит, общее число равновозможных исходов равно числу сочетаний из 16 по 2, т. е.
Пусть А — событие, при котором 2 выбранных велосипеда окажутся без дефектов. Любой выбор двух велосипедов из 16 является равновозможным исходом. Значит, общее число равновозможных исходов равно числу сочетаний из 16 по 2, т. е. 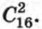 Исходом, благоприятным для события А, является выбор двух исправных велосипедов из имеющихся 12 исправных (16 - 4 = 12). Следовательно, число благоприятных для события А исходов равно
Исходом, благоприятным для события А, является выбор двух исправных велосипедов из имеющихся 12 исправных (16 - 4 = 12). Следовательно, число благоприятных для события А исходов равно 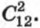 Отсюда получаем, что
Отсюда получаем, что

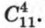 Все эти исходы равновозможны.
Все эти исходы равновозможны.
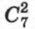 способами, а выбрать 2 девушек из 4 можно
способами, а выбрать 2 девушек из 4 можно 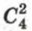 способами. Каждому выбору двух юношей соответствует
способами. Каждому выбору двух юношей соответствует 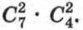 Отсюда получаем, что
Отсюда получаем, что

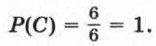
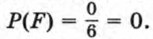
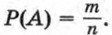 Так как m ≤ n, то
Так как m ≤ n, то 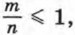 т. е. Р(А) ≤ 1. С другой стороны, всегда Р(А) ≥ 0. Следовательно, 0 ≤ Р(А) ≤ 1.
т. е. Р(А) ≤ 1. С другой стороны, всегда Р(А) ≥ 0. Следовательно, 0 ≤ Р(А) ≤ 1.
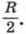 Площадь мишени равна πR2, а площадь центрального круга равна
Площадь мишени равна πR2, а площадь центрального круга равна 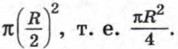 Значит, площадь кольцевой зоны равна
Значит, площадь кольцевой зоны равна 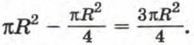 Вероятность того, что точка попадания дротика окажется в кольцевой зоне, равна отношению площади кольцевой зоны к площади мишени, т. е. равна
Вероятность того, что точка попадания дротика окажется в кольцевой зоне, равна отношению площади кольцевой зоны к площади мишени, т. е. равна