|
|
|
|
|
§ 12. Начальные сведения из теории вероятностей Вероятность равновозможных событий (окончание)Упражнения798. Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным? 799. Какова вероятность того, что при бросании игрального кубика выпадет: а) 1 очко; б) более 4 очков? 800. Ученик записал в тетради произвольное двузначное число. Какова вероятность того, что сумма цифр этого числа окажется равной 6? 801. В кооперативном доме 93 квартиры, из которых 3 находятся на первом этаже, а 6 — на последнем. Квартиры распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира, расположенная на первом или на последнем этаже? 802. Какова вероятность того, что при бросании двух кубиков сумма выпавших на них очков равна 3? 803. Андрей и Олег договорились, что если при бросании двух игральных кубиков в сумме выпадет число очков, кратное 5, то выигрывает Андрей, а если в сумме выпадет число очков, кратное 6, то выигрывает Олег. У кого из мальчиков больше шансов выиграть? 804. Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности идут 3 последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые четыре цифры, которые знал, и наугад комбинацию из цифр 1, 5 и 9. Какова вероятность того, что абонент набрал верный номер? 805. Чтобы открыть сейф, надо набрать в определенной последовательности пять цифр (без их повторения): 1, 2, 3, 4 и 5. Какова вероятность того, что если набирать цифры в произвольном порядке, то сейф откроется? 806. На четырех карточках написаны буквы «о», «т», «к», «р». Карточки перевернули и перемешали. Затем открыли наугад последовательно одну за другой эти карточки и положили их в ряд. Какова вероятность того, что получится слово «крот»? 807. В коробке лежат только красные и синие карандаши. Рассматриваются следующие события: А — из коробки вынут красный карандаш;
Вероятность какого из этих событий равна 0; равна 1; больше 0, но меньше 1? 808. Закинул старик в море невод. Рассматриваются следующие события: А — пришел невод с уловом рыбы;
Есть ли среди данных событий такие, вероятность которых равна 0; равна 1; больше 0, но меньше 1? 809. В ящике находится 10 деталей, одна из которых нестандартная. Наугад берут 2 детали. Какова вероятность того, что обе детали окажутся стандартными? 810. Четыре билета на елку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам? 811. В коробке лежит 8 красных карандашей и 4 синих. Из коробки наугад вынимают 5 карандашей. Какова вероятность того, что 3 из них окажутся красными, а 2 — синими? 812. На полке стоит 12 книг, из которых 4 — это учебники. С полки наугад снимают 6 книг. Какова вероятность того, что 3 из них окажутся учебниками? 813. Три подруги Аня, Вера и Маша отправились в театр. Получив в гардеробе номерки за три сданных пальто, они сложили их вместе. По окончании спектакля каждая из подруг взяла наугад один номерок и получила по нему пальто. Какова вероятность того, что: а) только Аня получила свое пальто;
814. В треугольнике АВС проведен отрезок DE, параллельный АВ (рис. 84). Известно, что 815. Пункты А и В находятся друг от друга на расстоянии 2,5 км. Телефонная линия, соединяющая эти пункты, оборвалась в неизвестном месте. Какова вероятность того, что точка разрыва удалена от точки А не более чем на 500 м? 816. На координатной прямой отмечены точки А(0) и В(3). На отрезке АВ наугад выбрана точка С(х). Какова вероятность того, что 0 ≤ х ≤ 1,2?
|
|
|



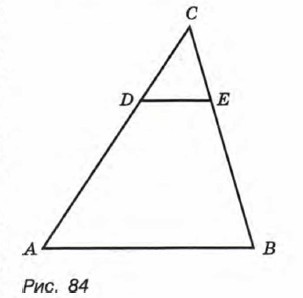
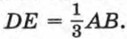 Какова вероятность того, что случайным образом выбранная точка треугольника АВС окажется принадлежащей треугольнику CDE?
Какова вероятность того, что случайным образом выбранная точка треугольника АВС окажется принадлежащей треугольнику CDE?