|
|
|
|
|
Для тех, кто хочет знать больше Сложение и умножение вероятностейРассмотрим пример. Пусть в коробке находится 19 шаров: 10 белых, 4 красных и 5 зеленых. Из коробки наугад вынимают один шар. Рассмотрим такие события: событие А — шар оказался красным;
События А и В не могут произойти вместе (одновременно). Говорят, что события А и В являются несовместными.
Пусть событие С означает, что извлеченный из коробки шар оказался не белым (красным или зеленым). Выясним, как вероятность события С связана с вероятностями каждого из событий А и В. Найдем вероятности событий А, В и С. Для каждого испытания (извлечение из коробки одного шара) равновозможными являются 19 исходов. Из них для события А благоприятными являются 4 исхода, для события В — 5 исходов, для события С — 9 исходов. Отсюда
Мы видим, что Р(С) = Р(А) + Р(В). Вообще
Пример 1. На карточках написали натуральные числа от 1 до 10 включительно, после чего карточки перевернули и перемешали. Затем наугад открыли одну карточку. Какова вероятность того, что на ней написано простое число или число, большее 7?
Р(С) = Р(А) + Р(В) = 0,4 + 0,3 = 0,7. При решении некоторых задач бывает удобно воспользоваться свойством вероятностей противоположных событий. Разъясним смысл понятия «противоположные события» на примере бросания игрального кубика. Пусть событие А означает, что выпало 6 очков, В — что выпало менее 6 очков. Всякое наступление события А означает ненаступление события В, а ненаступление события А — наступление события В. В таких случаях говорят, что А и В — противоположные события. Найдем вероятности событий А и В. Для события А благоприятным является один исход из шести равновозможных исходов, а для события В — пять исходов из шести. Значит,
Нетрудно заметить, что Р(А) + Р(В) = 1. Вообще
Действительно, пусть проводится некоторое испытание и рассматриваются два события: событие А и противоположное ему событие, которое принято обозначать События А и Р(А) + Р(
|
|
|



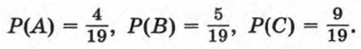
 Пусть событие А означает, что на карточке написано простое число, а событие В означает, что на карточке написано число, большее 7. Для события А благоприятными являются 4 исхода из 10 равновозможных (появление одного из чисел 2, 3, 5, 7), т. е. вероятность события А равна 0,4. Для события В благоприятными являются 3 исхода из 10 равновозможных (появление чисел 8, 9, 10), т. е. вероятность события В равна 0,3. Нас интересует событие С, когда на карточке написано простое число или число, большее 7. Событие С наступает тогда, когда наступает одно из событий А или В. Очевидно, что эти события являются несовместными. Значит, вероятность события С равна сумме вероятностей событий А и В, т. е.
Пусть событие А означает, что на карточке написано простое число, а событие В означает, что на карточке написано число, большее 7. Для события А благоприятными являются 4 исхода из 10 равновозможных (появление одного из чисел 2, 3, 5, 7), т. е. вероятность события А равна 0,4. Для события В благоприятными являются 3 исхода из 10 равновозможных (появление чисел 8, 9, 10), т. е. вероятность события В равна 0,3. Нас интересует событие С, когда на карточке написано простое число или число, большее 7. Событие С наступает тогда, когда наступает одно из событий А или В. Очевидно, что эти события являются несовместными. Значит, вероятность события С равна сумме вероятностей событий А и В, т. е.

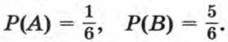
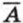 .
.