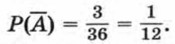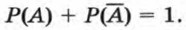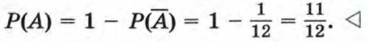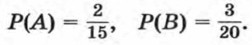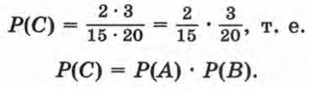|
|
|
|
|
Для тех, кто хочет знать больше Сложение и умножение вероятностей (продолжение)Пример 2. Бросают два игральных кубика. Какова вероятность того, что сумма очков, выпавших на двух кубиках, меньше 11?
(5; 6), (6; 5), (6; 6). Поэтому
Так как события А и
Отсюда
Рассмотрим теперь, как можно вычислить вероятность события, состоящего в совместном появлении двух независимых событий.
Приведем пример. Пусть в одном из двух ящиков находится 15 деталей, из которых 2 нестандартные, а в другом — 20 деталей, из которых 3 нестандартные. Из каждого ящика наугад вынимают по одной детали. Какова вероятность того, что обе детали окажутся нестандартными? Рассмотрим такие события: А — из первого ящика вынимают нестандартную деталь;
Для события А благоприятными являются 2 исхода из 15, а для события В благоприятными являются 3 исхода из 20. Значит,
Очевидно, что события А и В являются независимыми. Рассмотрим событие, состоящее в совместном появлении событий А и В. Обозначим его буквой С. Общее число равновозможных исходов испытания, в которых событие С наступает или не наступает, равно 15 • 20. Действительно, каждому из 15 извлечений детали из первого ящика соответствует 20 возможностей извлечения детали из второго ящика. Благоприятными для события С являются те исходы, при которых обе вынутые детали являются нестандартными. Каждому из двух возможных извлечений нестандартной детали из первого ящика соответствует три возможности извлечения нестандартной детали из второго ящика, т. е. число исходов, благоприятных для события С, равно 2 • 3. Следовательно,
Вообще
|
|
|



 Общее число равновозможных исходов этого испытания равно 36. Пусть событие А означает, что сумма очков, выпавших на двух кубиках, меньше 11. Так как благоприятным для события А является большое число исходов, то удобно сначала найти вероятность противоположного ему события
Общее число равновозможных исходов этого испытания равно 36. Пусть событие А означает, что сумма очков, выпавших на двух кубиках, меньше 11. Так как благоприятным для события А является большое число исходов, то удобно сначала найти вероятность противоположного ему события 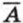 , которое означает, что сумма выпавших очков больше или равна 11. Благоприятными для события
, которое означает, что сумма выпавших очков больше или равна 11. Благоприятными для события