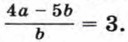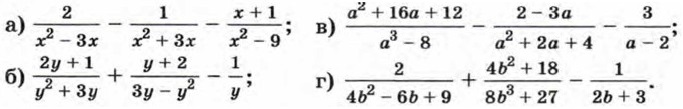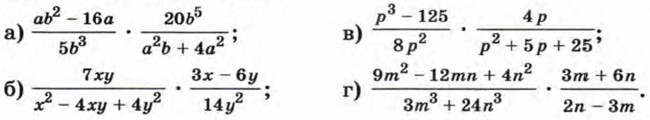|
Упражнения для повторения курса 7—9 классов



Тождественные преобразования
902. Преобразуйте в многочлен:
а) (х - 2у)(х + 2у) + 4у2;
б) (2а - 3b)(2а + 3b) - 3а2;
в) (5х - 1)2 + 10х;
г) (3у + 4z)2 - 8z(3y - 2z);
д) (m - 2n)(m2 + 2mn + 4n2) + 6n3;
е) (с2 + 4d)(c4 - 4c2d + 16d2) - с2(с4 - 1);
ж) (3х - 4у)2 - (2х - 7у)(4х + 2у);
з) 2х(2х + 3)2 - (2х - 3)(4х2 + 6х + 9).
903. Найдите значение выражения:
а) 8х2(х - 4) - (2х - 3)(4х2 + 6х + 9) - 17 при х = 0,5;
б) 4а2(3а - 2) - 3а(2а - 1)2 - (2а - 5)(2а + 5) при а = 3,3;
в) (9х2 - 3хb + b2)(3х + 6) - 9х(3х2 - 6) - b3 при 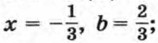
г) х(3х - 2у)(3х + 2у) - х(3х + 2у)2 + 2ху(5х + 2у) при х = 0,5, У = -1.
904. Докажите тождество:
а) (а + 2b)(а - 2b)(а2 + 4b2) = а4 - 16b4;
б) (х - 1)(х + 1)(х2 + 1)(х4 + 1) = х8 - 1;
в) (а - 2)(а + 2)(а2 - 2а + 4)(а2 + 2а + 4) = а6 - 64;
г) (с2 - с - 2)(с2 + с - 2) = с4 - 5с2 + 4.
905. Разложите на множители:
906. Разложите на множители:
|
а) х4 - 25у2;
б) 462 - 0,01с6;
в) 8а3 + с3;
|
г) х9 - 27;
д) 9аb2 - 16ас2;
е) -20ху3 + 45х3у.
|
907. Разложите на множители квадратный трехчлен:
|
а) х2 - х - 42;
б) у2 + 9у + 18;
в) 81х2 + 18х + 1;
|
г) 16b2 - 24b + 9;
д) 6х2 - х - 1;
е) 3а2 - 13а - 10.
|
908. Сократите дробь:
909. а) Найдите значение выражения 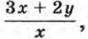 если известно, что если известно, что 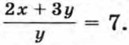
б) Найдите значение выражения 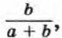 если известно, что если известно, что 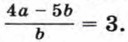
910. Упростите:
911. Представьте в виде дроби:
913. Упростите выражение:
Продолжение >>>
| 


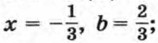
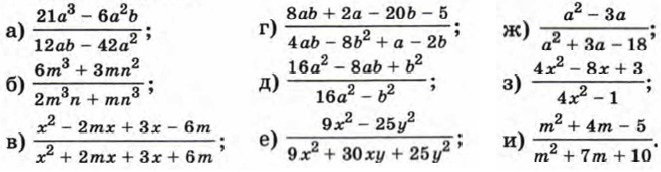
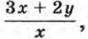 если известно, что
если известно, что 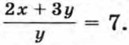
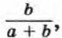 если известно, что
если известно, что