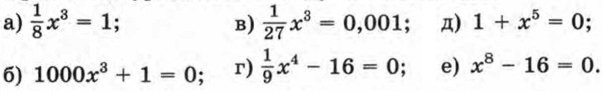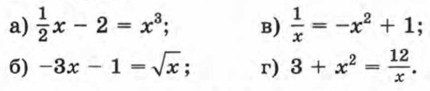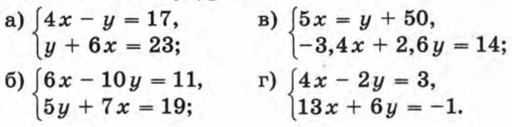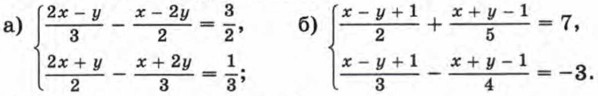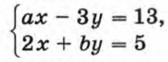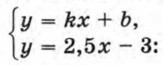|
|
|
|
|
Упражнения для повторения курса 7—9 классов Уравнения и системы уравнений (продолжение)945. Катер прошел 75 км по течению реки и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч? 946. Токарь должен был обработать 240 деталей к определенному сроку. Усовершенствовав резец, он стал обрабатывать в час на 2 детали больше, чем предполагалось по плану, и потому выполнил задание на 4 ч раньше срока. Сколько деталей в час должен был обрабатывать токарь? 947. Сотрудник типографии должен набрать к определенному сроку рукопись объемом 150 страниц. Если он будет набирать на 5 страниц в день больше, чем обычно, то закончит работу на 1 день раньше намеченного срока. Сколько страниц в день обычно набирает сотрудник? 948. Турист отправился на автомашине из города А в город В. Первые 75 км он ехал со скоростью, на 10 км/ч меньшей, чем рассчитывал, а остальной путь со скоростью, на 10 км/ч большей, чем рассчитывал. В город В, который удален от города А на 180 км, турист прибыл вовремя. С какой скоростью он ехал в конце пути? 949. Расстояние от станицы до железнодорожной станции равно 60 км. Мотоциклист выехал из станицы на 950. Из села в город, к которому ведет дорога длиной 120 км, выехала легковая автомашина. Через 30 мин из города в село выехал грузовик и встретился с легковой автомашиной в 45 км от города. Найдите скорость грузовика, если она меньше скорости легковой автомашины на 5 км/ч. 951. Решите уравнение:
952. Решите уравнение, введя новую переменную: а) 2(5x - 1)2 + 35л: -11 = 0;
953. Решите уравнение:
954. Приведите уравнение к виду хn = а и решите его:
955. Изобразив схематически графики, выясните, имеет ли уравнение корни:
956. Решите графически уравнение:
957. Решите систему уравнений:
958. Решите систему уравнений:
959. Решите систему уравнений
с переменными х и у, если одним из решений первого уравнения является пара чисел (8; 1), а второго — пара чисел (5; -1). 960. Каково расстояние от точки пересечения прямых 5х - 2у = -25 и -4х + 3у = 27: а) до оси абсцисс; б) до оси ординат; в) до начала координат? 961. Подберите значения k и b так, чтобы система уравнений
а) не имела решений;
962. Принадлежит ли точка пересечения прямых -2х + у = 11 и 3х + 2у = 1 прямой: а) 10х -Зу = -45; б) -1х + 9 у = 65? 963. Запишите уравнение прямой, которая проходит через точки: а) (0; 30) и (6; 0); б) (2; 3) и (-2; 10). 964. Найдите те значения а и b, при которых точки А(2; -3) и В(1; 4) принадлежат параболе у = ах2 + bх.
|
|
|



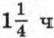 позже велосипедиста и прибыл на станцию, когда велосипедист был от нее в 21 км. Найдите скорость велосипедиста, если она была на 18 км/ч меньше скорости мотоциклиста.
позже велосипедиста и прибыл на станцию, когда велосипедист был от нее в 21 км. Найдите скорость велосипедиста, если она была на 18 км/ч меньше скорости мотоциклиста.