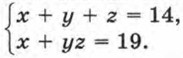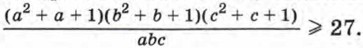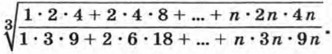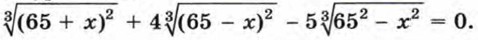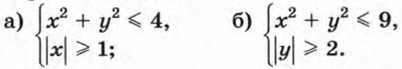Задачи повышенной трудности (окончание)

1080. Решите в натуральных числах систему уравнений

1081. Докажите, что при положительных значениях а, b и с верно неравенство

1082. Найдите при любом натуральном n значение выражения

1083. Докажите, что значение выражения

(5 + 10^{n + 1})(1 + 10 + ... + 10ⁿ) + 1

при любом натуральном n можно представить в виде квадрата натурального числа.

1084 Найдите наименьшее четырехзначное число, которое после умножения на 21 станет квадратом натурального числа.

1085. Трехзначное число х, кратное 5, можно представить в виде суммы куба и квадрата одного и того же натурального числа. Найдите число х.

1086. Взяли два различных натуральных числа. Эти числа сложили, перемножили, вычли из большего данного числа меньшее и разделили большее на меньшее. Оказалось, что сумма всех четырех результатов равна 441. Найдите эти числа.

1087. Найдите два натуральных числа, разность квадратов которых равна 45.

1088. Докажите, что не существует натурального числа, которое от перестановки первой цифры в конец числа увеличилось бы в 5 раз.

1089. Решите уравнение

1090. Постройте множество точек, координаты которых удовлетворяют неравенству:

а) ху² < х;
б) у² - х²у + 2х² > 2у;

в) х³ + ху² - 4х ≤ 0;
г) х²у + у³ - у ≥ 0.

1091. Изобразите множество точек, координаты которых удовлетворяют системе:

1092. В мешке содержится 2 черных и 2 белых шара. Рассматриваются события:

А — наугад извлеченные 2 шара оказываются одного цвета;
В — наугад извлеченные 2 шара оказываются разных цветов.

Игорь считает, что Р(А) = Р(В), а Олег считает, что Р(А) < Р(В). Кто из них прав?

1093. В мешке содержится 1 черный и 3 белых шара. Рассмотрите события:

Сравните Р(А) и Р(В).

1094. Находясь на даче у бабушки, Николай написал 3 письма Мише, Олегу и Пете. Письма он положил в конверты, надписал адреса и отправил по почте. Вечером он вспомнил, что не проверил, совпадает ли каждое письмо с соответствующим адресом. Рассмотрите следующие события:

А — все письма попадут к их адресатам;
В — ни одно письмо не попадет по назначению;
С — только одно из писем попадет по назначению;
D — только 2 письма попадут по назначению.

Найдите Р(А), Р(В), Р(С) и P(D).

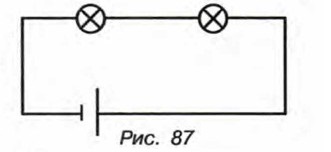
1095. Известно, что из 100 электрических лампочек 10 бракованных. Найдите вероятность того, что электрическая цепь, состоящая из двух соединенных последовательно лампочек (рис. 87), выбранных наугад, будет работать.

1096. B мешке содержится 5 черных, 4 красных и 3 белых шара. Последовательно из мешка наугад вынимают 3 шара, причем каждый извлеченный шар возвращают в мешок перед тем, как вынимают следующий. Найдите вероятность того, что первый шар окажется черным, второй — красным и третий — белым.

1097. Два человека стреляют по мишени. Вероятность поразить мишень первым стрелком равна 0,6, а вторым — 0,3. Какова вероятность того, что если каждый сделает по одному выстрелу, то в мишени окажется только одна пробоина?

<<< К началу Ответы >>>