Разложение квадратного трехчлена на множители

Пусть требуется разложить на множители квадратный трехчлен 3х² - 21x + 30. Вынесем сначала за скобки старший коэффициент 3. Получим

3х² - 21х + 30 = 3(х² - 7х + 10).

Для того чтобы разложить на множители трехчлен х² — 7х + 10, представим —7х в виде суммы одночленов -2х и -5х и применим способ группировки:

х² - 7х + 10 = х² - 2х - 5х + 10 =
= х(х - 2) - 5(х - 2) = (х - 2)(х - 5).

Значит,

3х² - 21х + 30 = 3(х - 2)(х - 5).

При х = 2 и х = 5 произведение 3(х - 2)(х - 5), а следовательно, и трехчлен 3х² - 21х + 30 обращаются в нуль. Значит, числа 2 и 5 являются его корнями.

Итак, мы представили квадратный трехчлен 3х² - 21х + 30 в виде произведения числа 3, т. е. старшего коэффициента, и двух линейных множителей. Первый из них представляет собой разность между переменной х и одним корнем трехчлена, а второй — разность между переменной х и другим корнем.

Такое разложение можно получить для любого квадратного трехчлена, имеющего корни. При этом считают, что если дискриминант квадратного трехчлена равен нулю, то этот трехчлен имеет два равных корня.

ТЕОРЕМА

Если x₁ и х₂ — корни квадратного трехчлена ах² + bх + с, то ах² + bх + с = а(х - x₁)(x - х₂).

Вынесем за скобки в многочлене ах² + bх + с множитель а.

Получим

Так как корни квадратного трехчлена ах² + bх + с являются корнями квадратного уравнения ах² + bх + с = 0, то по теореме Виэта

Поэтому

Итак,

ах² + bх + с = а(х - х₁)(х - х₂).

Покажем, что

если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.

Пусть квадратный трехчлен ах² + bх + с не имеет корней. Предположим, что его можно представить в виде произведения многочленов первой степени:

ах² + bх + с = (kx + m)(рх + q),

где k, m, р и q — некоторые числа, причем k ≠ 0 и р ≠ 0.

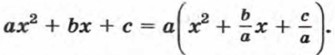
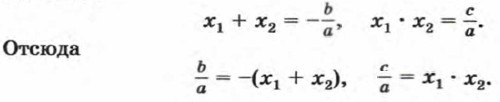
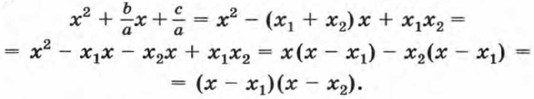
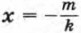Произведение (kx + m)(рх + q) обращается в нуль при и 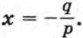Следовательно, при этих значениях х обращается в нуль и трехчлен ах² + bх + с, т. е. числа 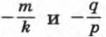являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.

Продолжение >>>