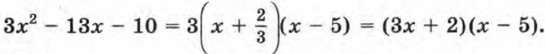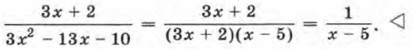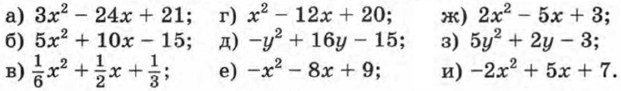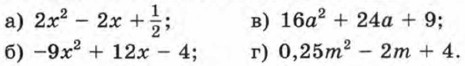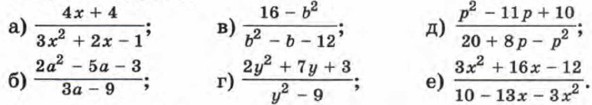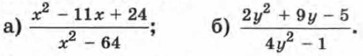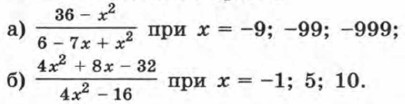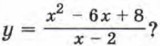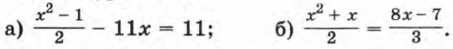|
|
|
|
|
§ 2. Квадратный трехчлен Разложение квадратного трехчлена на множители (продолжение)Пример 1. Разложим на множители квадратный трехчлен 2х2 + 7х - 4.
По теореме о разложении квадратного трехчлена на множители имеем
Полученный результат можно записать иначе, умножив число 2 на двучлен 2х2 + 7х - 4 = (2х - 1)(х + 4). Пример 2. Разложим на множители квадратный трехчлен -4x2 + 24х - 36.
Значит, -4х2 + 24x - 36 = -4(х - 3)(х - 3), или иначе -4x2 + 24х - 36 = -4(х - З)2. Пример 3. Сократим дробь
Его корни равны
Значит,
Упражнения76. Разложите на множители квадратный трехчлен:
77. Разложите на множители трехчлен:
78. Разложите на множители квадратный трехчлен:
79. Докажите тождество: а) 10х2 + 19х - 2 = 10(х - 0,1)(х + 2);
80. Можно ли представить квадратный трехчлен в виде произведения многочленов первой степени:
81. Можно ли разложить на множители квадратный трехчлен, коэффициенты которого — равные, отличные от нуля числа? 82. Покажите, что существует квадратный трехчлен, имеющий корни, коэффициенты которого — натуральные числа вида n, 2n, Зn (расположенные в произвольном порядке). Разложите этот трехчлен на множители. 83. Сократите дробь:
84. Сократите дробь:
85. Найдите значение дроби:
86. Чем различаются графики функций у = х - 4 и Повторение87. Решите уравнение:
88. Разложите на множители многочлен: а) 4х2 - 6х + 2ху - 3у; б) 4а3 + 2b3 - 2а2b - 4аb2. 89. В какой координатной четверти расположена точка пересечения графиков функций ƒ(x) = 0,8х + 2,1 и g(x) = -0,9х + 3?
|
|
|



 Решив уравнение 2х2 + 7х - 4 = 0, найдем корни трехчлена:
Решив уравнение 2х2 + 7х - 4 = 0, найдем корни трехчлена:
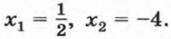
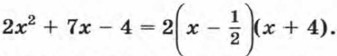
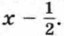 Получим
Получим

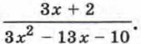
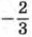 и 5. Поэтому
и 5. Поэтому