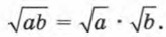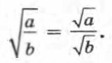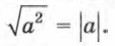|
|
|
|
|
Сведения из курса алгебры 7—8 классов
Выражения и их преобразования (окончание)10. Степень с целым показателем. Если n — натуральное число, большее 1, и а — любое число, то
Если n = 1 и а — любое число, то а1 = а. Если n = 0 и а — число, отличное от нуля, то а0 = 1. Если n — целое отрицательное число и а — отличное от нуля число, то
11. Свойства степени с целым показателем. а) аmаn = аm + n, где а ≠ 0, m и n — целые числа. При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. б) аm : аn = аm - n, где а ≠ 0, m и n — целые числа. При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. в) (аm)n = аmn, где а ≠ 0, m и n — целые числа. При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают. г) (ab)n = аnbn, где а^О и б^О, n — целое число. При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают. д) При возведении в степень дроби возводят в эту степень числитель и знаменатель и первый результат записывают в числителе, а второй — в знаменателе дроби. 12. Квадратным корнем из числа а называется число, квадрат которого равен а. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Арифметический квадратный корень из а обозначают √а. Выражение, стоящее под знаком корня, называют подкоренным выражением. Выражение √а имеет смысл для всех а ≥ 0 и не имеет смысла при а < 0. Свойства арифметического квадратного корня, а) Если а ≥ 0 и b ≥ 0, то
Корень из произведения неотрицательных множителей равен произведению корней из этих множителей, б) Если а ≥ 0 и b > 0, то
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя. в) При любом значении а верно равенство
|
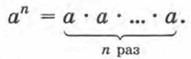
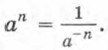
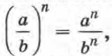где а = 0 и b ≠ 0, n — целое число.
|
|