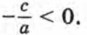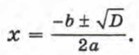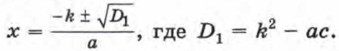|
|
|
|
|
Сведения из курса алгебры 7—8 классов Уравнения13. Корнем уравнения с одной переменной называется значение переменной, при котором уравнение обращается в верное равенство. Например, число 2 — корень уравнения х3 - х = 4х2 - 10, так как верно равенство 23 - 2 = 4 • 22 — 10. Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет. 14. Уравнения, в которых левая и правая части являются рациональными выражениями, называются рациональными. Если и левая и правая части рационального уравнения являются целыми выражениями, то уравнение называют целым. Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным. 15. Уравнения с одной переменной, имеющие одни и те же корни, называются равносильными. Например, уравнения х2 = 36 и (х - 6) (х + 6) = 0 равносильные. Каждое из них имеет два корня: -6 и 6. Уравнения, не имеющие корней, также считают равносильными. Уравнения обладают следующими свойствами: если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному. 16. Линейным уравнением с одной переменной называется уравнение вида ах = b, где х — переменная, а и b — числа. Число а называется коэффициентом при переменной, число b — свободным членом. Если а ≠ 0, то уравнение ах = b имеет единственный корень Например, уравнение 5х = 3 имеет корень 0,6. Если a ≠ 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 9 не имеет корней. Если а = 0 и b = 0, то корнем уравнения ах = b является любое число. 17. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где х — переменная, а, b и с — некоторые числа, причем а ≠ 0. Число а называют первым коэффициентом, b — вторым коэффициентом и с — свободным членом. Квадратное уравнение, в котором первый коэффициент равен 1, называют приведенным квадратным уравнением. 18. Если в квадратном уравнении ах2 + bх + с = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением. Неполное квадратное уравнение вида ах2 + bх = 0 имеет два корня: 0 и Неполное квадратное уравнение вида ах2 + с = 0 имеет два корня: Решают такие уравнения, сводя их к уравнениям вида х2 = m. Например, 0,5х2 - 18 = 0, 0,5х2 = 18, х2 = 36, x1 = -6, х2 = 6. 19. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называют выражение D = b2 - 4ас. Если D > 0, то квадратное уравнение имеет два корня; если D = 0, то один корень; если D < 0, то квадратное уравнение корней не имеет. Корни квадратного уравнения ах2 + bх + с = 0 при D ≥ 0 находят по формуле
Для квадратного уравнения вида ах2 + 2kx + с = 0 формулу корней можно записать так:
|
|
|



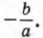 Такие уравнения обычно решают разложением его левой части на множители. Например, 3х2 - 15х = 3х (х - 5) = 0, х1 = 0 и х2 = 5.
Такие уравнения обычно решают разложением его левой части на множители. Например, 3х2 - 15х = 3х (х - 5) = 0, х1 = 0 и х2 = 5.
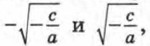 если
если 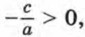 и не имеет корней, если
и не имеет корней, если