|
|
|
|
|
Сведения из курса алгебры 7—8 классов Выражения и их преобразования1. Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, называют целыми выражениями. При этом произведение одинаковых множителей может быть записано в виде степени. К целым выражениям относят и выражения, в которых, кроме действий сложения, вычитания и умножения, используется деление на число, отличное от нуля. Например, выражения а2 + 3аb - 2b2, (х - у)(2х + у2), Выражения, составленные из чисел и переменных, в которых, кроме действий сложения, вычитания и умножения, используется деление на выражение с переменными, называют дробными выражениями. Например, выражения Целые и дробные выражения называют рациональными выражениями. Целое выражение имеет смысл при любых значениях входящих в него переменных. Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных. 2. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных. Два выражения, принимающие равные значения при всех допустимых для них значениях переменных, называют тождественно равными, а замену одного выражения другим, тождественно равным ему, — тождественным преобразованием выражения. 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 8а3b, -1,5xy2z8, 12, с, m10 — одночлены. Степенью одночлена называется сумма показателей степеней всех входящих в него переменных. Например, степень одночлена 9а7b равна 8. 4. Многочленом называется сумма одночленов. Например, у4 - 8у3 + 2у - 3, 4а4b + 11а2b2 - ab + 3b - 1 — многочлены. Одночлены считают многочленами, состоящими из одного члена. Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 18а6 - 7а4b3 + 1 равна степени одночлена -7а4b3, т. е. равна 7. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида. 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки. Например, (5х2 - 3ху) + (4ху - 2х2 + 1) = 5x2 - 3ху + 4ху - 2х2 + 1 = 3х2 + ху + 1. При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки. Например, (8а2 - 3аb) - (7а2 - 4аb + 5) = 8а2 - 3ab - 7а2 + 4ab - 5 = а2 + ab - 5. Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например, 2x2(3х3 - ху + 5у2) = 6x5 - 2х3у + 10х2у2. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например, (2а - 3)(3а2 + а - 4) = 6а3 + 2а2 - 8а - 9а2 - 3а + 12 = 6а3 - 7а2 - 11а + 12. Любое целое выражение можно представить в виде многочлена.
|
|
|



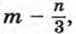 а2 : 7 целые.
а2 : 7 целые.
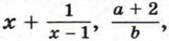 5m : n дробные.
5m : n дробные.
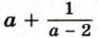 не имеет смысла при а = 2, выражение
не имеет смысла при а = 2, выражение 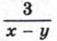 не имеет смысла при х = у.
не имеет смысла при х = у.