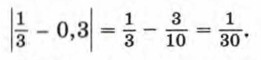|
|
|
|
|
Сведения из курса алгебры 7—8 классов Действительные числа. Приближенные вычисления41. Целые и дробные числа составляют множество рациональных чисел. Всякое рациональное число можно представить в виде дроби Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Положительные бесконечные десятичные дроби, противоположные им числа и число нуль образуют множество действительных чисел. Число, которое можно представить в виде бесконечной десятичной непериодической дроби, называют иррациональным числом. Каждому действительному числу соответствует точка на координатной прямой, и каждой точке координатной прямой соответствует некоторое действительное число. 42. Стандартным видом числа α называют его запись в виде a • 10n, где 1 ≤ а < 10 и n — целое число, число п называют порядком числа. Например, 73 000 = 7,3 • 104; 0,0026 = 2,6 • 10-3. 43. Абсолютной погрешностью приближенного значения числа называется модуль разности точного и приближенного значений. Например, абсолютная погрешность приближенного значения 0,3 числа
Если абсолютная погрешность приближенного значения не превосходит некоторого числа h, то это значение называют приближенным значением с точностью до Л. Например, 1,41 является приближенным значением 42 с точностью до 0,01. Если число х равно а с точностью до h, то пишут: х = а ± h. При этом число h обычно берут с одной или двумя значащими цифрами. Например, √3 = 1,73 + 0,01. 44. Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения. Относительную погрешность обычно выражают в процентах. Например, при округлении дроби 25,4 до единиц получается приближенное значение 25. Его относительная погрешность равна
|
|
|



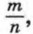 где m — целое число, а n — натуральное.
где m — целое число, а n — натуральное.
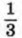 равна
равна