|
|
|
|
|
Сведения из курса алгебры 7—8 классов Функции33. Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Независимую переменную х иначе называют аргументом, а о зависимой переменной у говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. 34. Линейной функцией называется функция, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа. Ее областью определения является множество всех действительных чисел. Графиком линейной функции является прямая. Число к называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b. Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b — параллельна оси х; если к = 0 и b = 0, то график функции совпадает с осью х. 35. Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы. 36. Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью. График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, при k < 0 — во второй и четвертой координатных четвертях. 37. Обратной пропорциональностью называется функция, которую можно задать формулой вида При к > 0 функция При k < 0 функция График обратной пропорциональности — гипербола. При k > 0 график расположен в первой и третьей координатных четвертях, при k < 0 — во второй и четвертой координатных четвертях. 38. Областью определения функции у = х2 является множество всех действительных чисел. Функция обращается в нуль при х = 0, а при х ≠ 0 принимает положительные значения. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у. 39. Областью определения функции у = х3 является множество всех действительных чисел. Функция обращается в нуль при х = 0, принимает отрицательные значения, если х < 0, и положительные значения, если х > 0. График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат. 40. Область определения функции у = -√x — множество всех неотрицательных чисел. Функция обращается в нуль при х = 0, при х > 0 функция принимает положительные значения. График функции у = у√х расположен в первой координатной четверти, он представляет собой ветвь параболы.
|
|
|



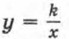 , где х — независимая переменная, k — не равное нулю число. Областью определения функции является множество всех действительных чисел, отличных от нуля.
, где х — независимая переменная, k — не равное нулю число. Областью определения функции является множество всех действительных чисел, отличных от нуля.