|
|
|
|
|
§ 3. Квадратичная функция и ее график Графики функций у = ах2 + n и у= а(х - m)2 (продолжение)Пример 3. Рассмотрим функцию
Для построения графика функции
Построим график функции Значит, если переместить каждую точку графика функции Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси х. График функции
Полученные выводы позволяют понять, что представляет собой график функции у = а(х - m)2 + n. Рассмотрим, например, функцию
Заметим, что производить параллельные переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль оси х, а затем вдоль оси у или наоборот. Полученные нами выводы о преобразовании графиков применимы к любым функциям. График функции у = ƒ(x) + n можно получить из графика функции у = ƒ(x) с помощью параллельного переноса вдоль оси у на п единиц вверх, если n > 0, или на -n единиц вниз, если n < 0. График функции у = ƒ(x - m) можно получить из графика функции у = ƒ(x) с помощью параллельного переноса вдоль оси х на m единиц вправо, если m > 0, или на -m единиц влево, если m < 0. График функции у = ƒ(x - m) + n можно получить из графика функции у = ƒ(x) с помощью двух соответствующих параллельных переносов.
При вращении параболы вокруг ее оси получается фигура, которую называют параболоидом. Если внутреннюю поверхность параболоида сделать зеркальной и направить на нее пучок лучей, параллельных оси симметрии параболы, то отраженные лучи соберутся в одной точке, которую называют фокусом. В то же время если источник света поместить в фокусе, то отраженные от зеркальной поверхности параболоида лучи окажутся параллельными и не рассеиваются. Первое свойство позволяет получить в фокусе параболоида высокую температуру. Согласно легенде это свойство использовал древнегреческий ученый Архимед (287-212 гг. до н. э.). При защите Сиракуз в войне против римлян он построил систему параболических зеркал, которая позволила сфокусировать отраженные солнечные лучи на кораблях римлян. В результате температура в фокусах параболических зеркал оказалась настолько высокой, что на кораблях вспыхнул пожар и они сгорели. Второе свойство используется, например, при изготовлении прожекторов и автомобильных фар.
|
|
|



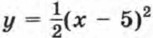 и выясним, что представляет собой ее график.
и выясним, что представляет собой ее график.
 Для этого в одной системе координат построим графики функции у = 2х и
Для этого в одной системе координат построим графики функции у = 2х и 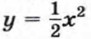 воспользуемся таблицей (1). Составим теперь таблицу значений функции
воспользуемся таблицей (1). Составим теперь таблицу значений функции 
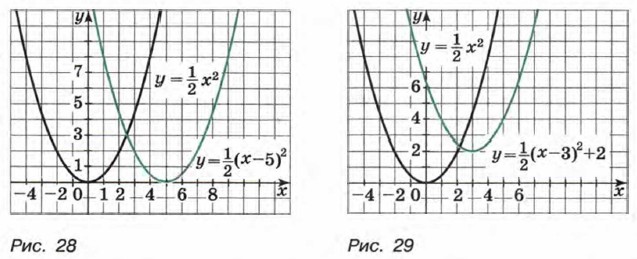

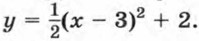 Ее график можно получить из графика функции
Ее график можно получить из графика функции 