|
|
|
|
|
§ 3. Квадратичная функция и ее график Графики функций у = ах2 + n и у= а(х - m)2Рассмотрим другие частные случаи квадратичной функции. Пример 1. Выясним, что представляет собой график функции
Составим таблицу значений функции
График функции Чтобы получить таблицу значений функции Составим таблицу значений функции
Построим точки, координаты которых указаны в таблице (2), и соединим их плавной линией. Получим график функции Легко понять, что каждой точке (х0; у0) графика функции График функции
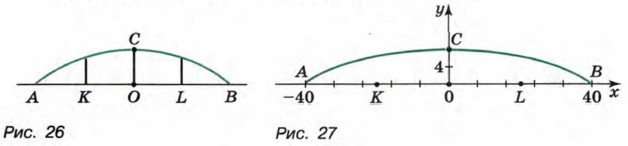
Пример 2. Арка моста имеет форму параболы (рис. 26). Мост удерживают три опоры, расположенные на одинаковом расстоянии друг от друга. Найдем длины этих опор, если известно, что АВ = 80 м, ОС = 8 м, АК = КО = OL = LB.
А(-40; 0), Б(40; 0), С(0; 8). Вершиной параболы является точка С(0; 8). Значит, n = 8. Для отыскания коэффициента а подставим в уравнение у = ах2 + 8 координаты точки В(40; 0): 0 = а • 1600 + 8. Отсюда у = -0,005x2 + 8. Теперь нетрудно найти длины опор: если x = -20, то у = 6; если х = 0, то у = 8;
Значит, опоры моста имеют длины 6 м, 8 м и 6 м.
|
|
|



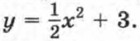
 С этой целью в одной системе координат построим графики функций
С этой целью в одной системе координат построим графики функций 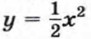 и
и 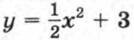 .
.

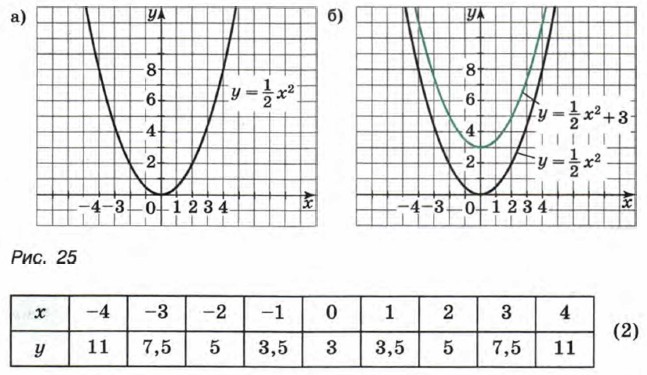

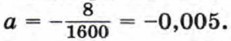 Мы получили уравнение параболы
Мы получили уравнение параболы