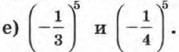|
|
|
|
|
§ 4. Степенная функция. Корень n-й степени Функция у = хn (продолжение)Докажем свойство 4. Доказательство того, что функция возрастает в промежутке [0; +∞), такое же, как для степенной функции с четным показателем. Докажем, что функция возрастает так же и в промежутке (-∞; 0]. Пусть х1 и х2 принадлежат этому промежутку и х2 > х1. Тогда 0 ≤ -х2 < -x1. Так как -х2 ≥ 0 и -х1 > 0, то (-x2)n < (-x1)n. В силу нечетности числа n заключаем, что Если же x1 < 0, а х2 > 0, то очевидно, что Свойство 5 следует из свойств 1—3 и из того, что любое неотрицательное число является значением степенной функции с натуральным показателем при некотором х ≥ 0. График функции пересекает любая прямая у = а.
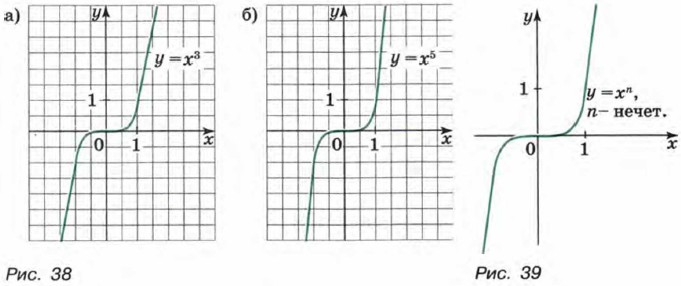
На рисунке 38 изображены графики функций у = х3 и у = х5. На рисунке 39 показано, как выглядит график функции у = хn с нечетным показателем n > 1. Упражнения136. Функция задана формулой у = х36. Сравните с нулем значение этой функции при х = -5; 0; 3. 137. Сравните с нулем значение функции у = х49 при х = -9; 0; 7. 138. Функция задана формулой ƒ(х) = х20. Сравните:
139. Функция задана формулой g(х) = х35. Сравните:
140. Сравните:
141. Сравните:
142. Проходит ли график функции у = х5 через точку А(3; 243)? В(-3; 243)? С(5; 3125)? 143. Принадлежит ли графику функции у = х7 точка А(2; 128)? В(-2; -128)? С(-3; 2187)? 144. Используя калькулятор, найдите с точностью до 0,01 значение функции у = х5 при: а) х = 0,72; б) х = 2,6; в) х = -3,4. 145. Изобразите схематически график функции:
146. В каких координатных четвертях расположен график функции: а) у = х40; б) у = х123? 147. Пользуясь рисунком 37 или 39, выясните, сколько решений имеет уравнение:
|
|
|



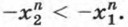 Отсюда
Отсюда 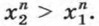 Значит, функция возрастает и в промежутке (-∞; 0].
Значит, функция возрастает и в промежутке (-∞; 0].
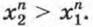 Значит, функция возрастает на всей области определения. График функции с возрастанием х поднимается вверх.
Значит, функция возрастает на всей области определения. График функции с возрастанием х поднимается вверх.