|
|
|
|
|
§ 4. Степенная функция. Корень n-й степени Функция у = хnРассмотрим функцию, заданную формулой у = хn, где х — независимая переменная, а n — натуральное число. Такую функцию называют степенной функцией с натуральным показателем. Степенные функции при n = 1, 2 и 3, т. е. функции у = х, у = х2 и у = х3, мы уже рассматривали. Их свойства и графики нам известны. Выясним теперь свойства степенной функции и особенности ее графика при любом натуральном n. Выражение хn, где n — натуральное число, имеет смысл при любом х. Поэтому областью определения степенной функции с натуральным показателем является множество всех действительных чисел. Сначала рассмотрим случай, когда показатель n — четное число. Свойства функции у = хn при четном n аналогичны свойствам функции у = х2.
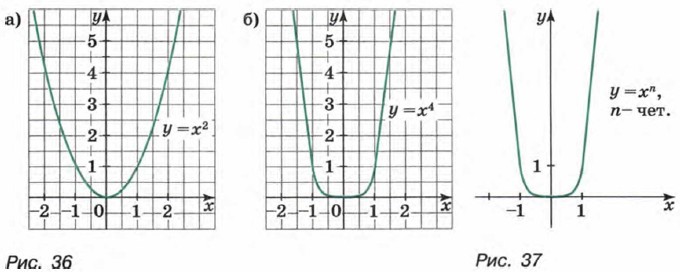
Докажем свойство 4. Пусть х1 и х2 принадлежат промежутку [0; +∞) и х2 > х1. Если х1 = 0, то очевидно, что С возрастанием х график функции слева от начала координат опускается вниз, а справа поднимается вверх. Остановимся теперь на свойстве 5. Мы установили, что при любом х и четном n функция принимает неотрицательные значения. Можно доказать, что любое неотрицательное число является значением степенной функции с натуральным показателем при некотором х ≥ 0. Значит, область значений функции — промежуток [0; +∞). График функции пересекает любая прямая у = а, если а ≥ 0. Если же а < 0, то прямая у = а не пересекает график. На рисунке 36 изображены графики функций у = х2 и у = x4. На рисунке 37 показано, как выглядит график функции у = хn с четным показателем n.
Рассмотрим теперь свойства степенной функции у = хn при нечетном n. Эти свойства аналогичны свойствам функции у = x3.
|
|
|



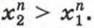 Если х1 > 0, то, перемножив почленно n одинаковых неравенств х2 > х1 с положительными членами, получим верное неравенство
Если х1 > 0, то, перемножив почленно n одинаковых неравенств х2 > х1 с положительными членами, получим верное неравенство 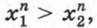 т. е.
т. е. 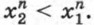 Значит, в промежутке (-∞; 0] функция убывает.
Значит, в промежутке (-∞; 0] функция убывает.