|
|
|
|
|
§ 2. Простейшие задачи в координатах Простейшие задачи в координатахВведение системы координат даёт возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат. Решим три вспомогательные задачи а) — в). а) Координаты середины отрезка. Пусть в системе координат Оху точка А имеет координаты (х1; у1), а точка В — координаты (х2; у2). Выразим координаты (х; у) середины С отрезка АВ через координаты его концов. Так как точка С — середина отрезка АВ, то
(Это равенство было доказано в п. 87.) Координаты векторов
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов. б) Вычисление длины вектора по его координатам. Докажем, что длина вектора
Отложим от начала координат вектор
Но в) Расстояние между двумя точками. Пусть точка М1 имеет координаты (х1; у1), а точка М2 — координаты (х2; у2). Выразим расстояние d между точками М1 и М2 через их координаты. Рассмотрим вектор
Но
|
|
|



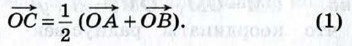
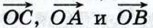 равны соответствующим координатам точек С, А к В:
равны соответствующим координатам точек С, А к В: 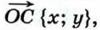
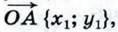
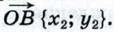 Записывая равенство (1) в координатах, получим:
Записывая равенство (1) в координатах, получим:
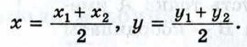
 (x; у) вычисляется по формуле
(x; у) вычисляется по формуле

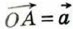 и проведём через точку А перпендикуляры АА1 и АА2 к осям Ох и Оу (рис. 280). Координаты точки А равны координатам вектора
и проведём через точку А перпендикуляры АА1 и АА2 к осям Ох и Оу (рис. 280). Координаты точки А равны координатам вектора 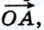 т. е. (х; у). Поэтому ОА1 = |х|, АА1 = ОА2 = |y| (мы рассматриваем случаи, когда х ≠ 0 и у ≠ 0; другие случаи рассмотрите самостоятельно). По теореме Пифагора
т. е. (х; у). Поэтому ОА1 = |х|, АА1 = ОА2 = |y| (мы рассматриваем случаи, когда х ≠ 0 и у ≠ 0; другие случаи рассмотрите самостоятельно). По теореме Пифагора


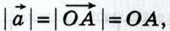 поэтому
поэтому 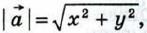 что и требовалось доказать.
что и требовалось доказать.
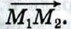 Его координаты равны {х2 - х1, у2 - y1}. Следовательно, длина этого вектора может быть найдена по формуле
Его координаты равны {х2 - х1, у2 - y1}. Следовательно, длина этого вектора может быть найдена по формуле

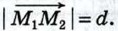 Таким образом, расстояние d между точками М1 (x1; у1) и М2 (х2; у2) выражается формулой
Таким образом, расстояние d между точками М1 (x1; у1) и М2 (х2; у2) выражается формулой
