|
|
|
|
|
§ 2. Простейшие задачи в координатах Задачи к § 2. Простейшие задачи в координатах929. 930. 931. Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (-3; 3), а диагонали квадрата пересекались в начале координат. Найдите координаты точек М, N и Q. 932. Найдите координаты вершин равнобедренного треугольника АВС, изображённого на рисунке 281, если АВ = 2а, а высота СО рис 281 равна h.
933. 934. 935.
936.
937. 938. 939. 940. 941. 942. 943. Точки B и С лежат соответственно на положительных полуосях Ох и Оу, а точка А лежит на отрицательной полуоси Ох, причём ОА = а, OB = b, OC = h. Найдите стороны АС и ВС треугольника АВС. 944. Вершина А параллелограмма ОАСВ лежит на положительной полуоси Ох, вершина В имеет координаты (6; с), а ОА = а. Найдите: а) координаты вершины С; б) сторону АС и диагональ СО. 945. Найдите сторону АС и диагональ ОС трапеции ОВСА с основаниями ОА = а и ВС = d, если точка А лежит на положительной полуоси Ох, а вершина В имеет координаты (b; с). 946. Найдите х, если: а) расстояние между точками А (2; 3) и В (х; 1) равно 2; б) расстояние между точками М1 (-1; х) и М2 (2х; 3) равно 7. 947. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты: а) А (0; 1), В (1; -4), С (5; 2); б) А (-4; 1), В (-2; 4), С (0; 1). 94. На оси ординат найдите точку, равноудалённую от точек: а) А (-3; 5) и B (6; 4); б) С (4; -3) и D (8; 1). 949. На оси абсцисс найдите точку, равноудалённую от точек: а) А (1; 2) и B (-3; 4); б) С (1; 1) и B (3; 5). 950. Докажите, что четырёхугольник MNPQ является параллелограммом, и найдите его диагонали, если: а) М (1; 1), (6; 1), B (7; 4), Q (2; 4);
951. Докажите, что четырёхугольник ABCD является прямоугольником, и найдите его площадь, если: а) А (-3; -1), B (1; -1), С (1; -3), D (-3; -3);
|
|
|



 Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин треугольника АВО, если: а) ОА = 5, ОВ = 3; б) ОА = а, ОВ = b.
Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин треугольника АВО, если: а) ОА = 5, ОВ = 3; б) ОА = а, ОВ = b.

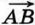 , зная координаты его начала и конца: а) А (2; 7), В (-2; 7); б) А (-5; 1), В (-5; 27); в) А (-3; 0), В (0; 4); г) А (0; 3), В (-4; 0).
, зная координаты его начала и конца: а) А (2; 7), В (-2; 7); б) А (-5; 1), В (-5; 27); в) А (-3; 0), В (0; 4); г) А (0; 3), В (-4; 0).