|
|
|
|
|
§ 3. Уравнения окружности и прямой Задачи к § 3. Уравнения окружности и прямой959. Начертите окружность, заданную уравнением: а) х2 + у2 = 9; б) (х - 1)2 + (у + 2)2 = 4; в) (х + 5)2 + (у - 3)2 = 25; г) (х - 1)2 + у2 = 4; д) х2 + (у + 2)2 = 2. 960. а) х2 + у2 = 25; б) (х - 1)2 + (у + 3)2 = 9; 961. а) внутри круга, ограниченного данной окружностью;
962. Даны окружность х2 + у2 = 25 и две точки А (3; 4) и В (4;-3). Докажите, что АВ — хорда данной окружности. 963. На окружности, заданной уравнением х2 + у2 = 25, найдите точки: а) с абсциссой -4; б) с ординатой 3. 964. 965. Напишите уравнения окружностей с центром в начале координат и радиусами r1 = 3, 966. Напишите уравнение окружности радиуса r с центром А, если: а) А (0; 5), r = 3; б) А (-1;2), r = 2; в) А (-3;-7), 967. 968. 969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5), N (7; -3); б) М (2; -1), N (4; 3). 970. Напишите уравнение окружности, проходящей через точку А (1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5. Сколько существует таких окружностей? 971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и В (0; 9), если известно, что центр окружности лежит на оси ординат. 972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2); б) С (2; 5) и D (5; 2); в) М (0; 1) и N (-4; -5). Решение а) Уравнение прямой АВ имеет вид ах + by + с = 0. Так как точки А и В лежат на прямой АВ, то их координаты удовлетворяют этому уравнению: а • 1 + b • (-1) + с = 0, а • (-3) + b • 2 + с = 0,
Из этих уравнений выразим коэффициенты а и b через с: а = 3с, b = 4с. Подставив эти значения в уравнение прямой, получим 3сх + 4су + с = 0. При любом с ≠ 0 это уравнение является уравнением прямой АВ. Сократив на с, запишем искомое уравнение в виде 3х + 4у + 1 = 0. 973. 974. 975. Найдите координаты точек пересечения прямой 3х - 4у + 12 = О с осями координат. Начертите эту прямую. 976. 977. 978. Начертите прямую, заданную уравнением: а) у = 3; б) х = -2; в) у = -4; г) х = 7. 979. 980 Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см, если известно, что его диагонали лежат на осях координат.
|
|
|



 Какие из точек А (3; -4), В (1; 0), С (0; 5), D (0; 0) и Е (0; 1) лежат на окружности, заданной уравнением:
Какие из точек А (3; -4), В (1; 0), С (0; 5), D (0; 0) и Е (0; 1) лежат на окружности, заданной уравнением:
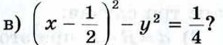
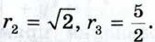
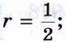 г) А (4;-3), r =10.
г) А (4;-3), r =10.