|
|
|
|
|
§ 3. Уравнения окружности и прямой Взаимное расположение двух окружностей (окончание)Итак, если система уравнений (4) имеет решение, то величина d удовлетворяет неравенствам (7). Поэтому, если не выполнено какое-то из неравенств (7), то система (4) не имеет решений и, следовательно, данные окружности не имеют общих точек. Так будет в двух случаях: 1) d < R - r, т. е. d + r < R (рис. 288, в). В этом случае окружность радиуса r лежит внутри круга радиуса Д. Говорят также, что одна окружность лежит внутри другой. 2) d > R + r (рис. 288, г). В этом случае говорят, что одна окружность лежит вне другой. Если неравенства (7) выполнены, то возможны три случая: 3) d = R - r, при этом R > r, поскольку d > 0. Как уже было отмечено, в этом случае x0 = R, поэтому из первого из равенств (5) следует, что y0 = 0. Непосредственной проверкой можно убедиться в том, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае окружности имеют ровно одну общую точку, и их взаимное расположение изображено на рисунке 288, д. Говорят, что окружности касаются изнутри. 4) d = R + r. В этом случае также х0 = R, поэтому y0 = 0, и непосредственно проверяется, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае, как и в случае 3, окружности имеют ровно одну общую точку, но их взаимное расположение иное (рис. 288, е). Говорят, что окружности касаются извне. 5) R - r < d < R+ r. Как уже было отмечено, в этом случае число х0, определённое равенством (6), удовлетворяет неравенству x0 < R, поэтому из первого равенства (5) получаем два значения у0: Таким образом, если d ≠ 0, то возможны пять случаев взаимного расположения двух окружностей (см. рис. 288, б—е).
|
|
|



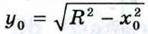 и
и 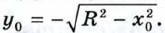 Нетрудно убедиться в том, что система (4) имеет в данном случае два решения: х = х0,
Нетрудно убедиться в том, что система (4) имеет в данном случае два решения: х = х0,