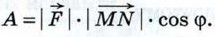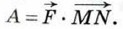|
|
|
|
|
§ 3. Скалярное произведение векторов Скалярное произведение векторовМы знаем, как выполняется сложение векторов и умножение вектора на число. Введём ещё одно действие над векторами — скалярное умножение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение векторов По определению
Если векторы Таким образом, скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Из формулы (1) также следует, что скалярное произведение ненулевых векторов На рисунке 302 Если
Скалярное произведение Скалярное произведение векторов широко используется в физике. Например, из курса механики известно, что работа А постоянной силы
Правая часть этого равенства представляет собой скалярное произведение векторов
|
|
|



 и
и  обозначается так:
обозначается так: 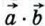 или
или 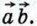
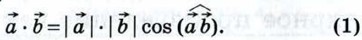
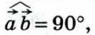 то
то 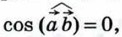 и поэтому
и поэтому 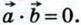 Обратно: если
Обратно: если 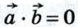 и векторы
и векторы 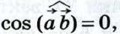 и, следовательно,
и, следовательно, 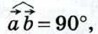 т. е. векторы
т. е. векторы 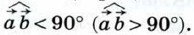
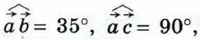
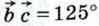 поэтому
поэтому 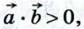
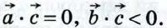
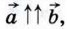 то по формуле (1) получаем
то по формуле (1) получаем 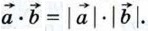 В частности,
В частности,
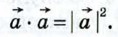

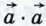 называется скалярным квадратом вектора
называется скалярным квадратом вектора 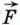 при перемещении тела из точки М в точку N (рис. 303) равна произведению длин векторов силы
при перемещении тела из точки М в точку N (рис. 303) равна произведению длин векторов силы 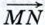 на косинус угла между ними:
на косинус угла между ними: