Третий признак равенства треугольников

Теорема

Если три стороны одного треугольника соответ ственно равны трём сторонам другого треуголь ника, то такие треугольники равны.

Доказательство

Рассмотрим треугольники АВС и A₁B₁C₁, у которых АВ = А₁В₁, ВС = В₁С₁, СА = С₁А₁ (рис. 69). Докажем, что АВС = А₁В₁С₁. Приложим треугольник АВС к треугольнику A₁B₁C₁ так, чтобы вершина А совместилась с вершиной А₁, вершина В — с вершйной В₁, а вершины С и С₁ оказались по разные стороны от прямой A₁B₁ (рис. 70).

треугольники

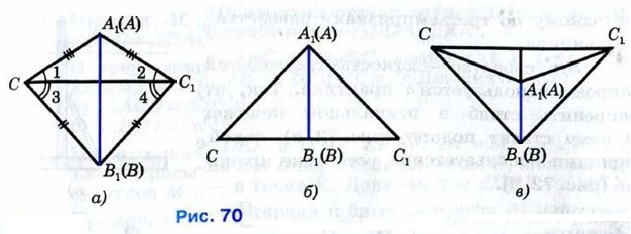
Третий признак
равенства треугольников

Возможны три случая: луч С₁С проходит внутри угла А₁С₁В₁ (рис. 70, а); луч С₁С совпадает с одной из сторон этого угла (рис. 70, б); луч С₁С проходит вне угла А₁С₁В₁ (рис. 70, в). Рассмотрим первый случай (остальные случаи рассмотрите самостоятельно).

Так как по условию теоремы стороны АС и А₁С₁, ВС и В₁С₁ равны, то треугольники А₁С₁С и В₁С₁С — равнобедренные (см. рис. 70, а). По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠A₁CB₁ = ∠A₁C₁B₁. Итак, АС = А₁С₁, ВС = В₁С₁, ∠C = ∠C₁.

Следовательно, треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников. Теорема доказана.

Окончание >>>