|
|
|
|
|
VI. Площадь Дополнительные задачи к главе VI (продолжение)517. Найдите площадь четырёхугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA = 15 см, АС = 12 см. 518. Найдите площадь равнобедренной трапеции, если: а) её меньшее основание равно 18 см, высота — 9 см и острый угол равен 45°; б) её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны. 519. Найдите площадь равнобедренной трапеции, у которой высота равна h, а диагонали взаимно перпендикулярны. 520. Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма оснований равна 2а. Найдите площадь трапеции. 521. Докажите, что если диагонали четырёхугольника ABCD взаимно перпендикулярны, то AD2 + ВС2 = АВ2 + CD2. 522. В равнобедренной трапеции ABCD с основаниями AD = 17 см, ВС = 5 см и боковой стороной АВ = 10 см через вершину В проведена прямая, делящая диагональ АС пополам и пересекающая основание AD в точке М. Найдите площадь треугольника BDM. 523. Два квадрата со стороной а имеют одну общую вершину, причём сторона одного из них лежит на диагонали другого. Найдите площадь общей части этих квадратов. 524. Стороны треугольника равны 13 см, 5 см и 12 см. Найдите площадь этого треугольника. 525. Расстояние от точки М, лежащей внутри треугольника АВС, до прямой АВ равно 6 см, а до прямой АС равно 2 см. Найдите расстояние от точки М до прямой ВС, если АВ=13см, ВС = 14 см, АС = 15 см. 526. В ромбе высота, равная 527. В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции. 528. В трапеции ABCD диагонали пересекаются в точке О. Найдите площадь треугольника АОВ, если боковая сторона CD трапеции равна 12 см, а расстояние от точки О до прямой CD равно 5 см. 529. Диагонали четырёхугольника равны 16 см и 20 см и пересекаются под углом в 30°. Найдите площадь этого четырёхугольника. 530. В равнобедренном треугольнике АВС с основанием ВС высота AD равна 8 см. Найдите площадь треугольника АВС, если медиана DM треугольника ADC равна 8 см. 531. Стороны АВ и ВС прямоугольника ABCD равны соответственно 6 см и 8 см. Прямая, проходящая через вершину С и перпендикулярная к прямой BD, пересекает сторону AD в точке М, а диагональ BD — в точке К. Найдите площадь четырёхугольника АВКМ. 532. В треугольнике АВС проведена высота ВН. Докажите, что если: а) угол А острый, то ВС2 = АВ2 + АС2 - 2АС • АН;
|
|
|



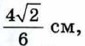 составляет
составляет 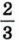 большей диагонали. Найдите площадь ромба.
большей диагонали. Найдите площадь ромба.