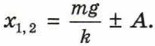|
|
|
|
|
§ 13. Более сложные вопросы колебаний Ответы к § 13: Более сложные вопросы колебаний1. 0,8 с. 2. 0,64 Гц. 3. 3,5 Гц. 4. 5. 114 мДж. 6. 45 км/ч. Указание. Наиболее сильное раскачивание будет наблюдаться при резонансе, когда частота толчков совпадает с собственной частотой колебаний маятника. 7. 0,51 м. 8. 9. 9. 10. В начале падения сопротивлением воздуха можно пренебречь (лифт падает свободно), поэтому в лифте возникает невесомость. Это равносильно «выключению» силы тяжести, а вместе с ней — и силы, возвращающей маятник к положению равновесия. Значит, скорость маятника будет оставаться постоянной по модулю. В частности, если в начальный момент маятник находился в крайнем положении, он так и застынет в этом положении; если же в начальный момент маятник двигался, он будет равномерно двигаться по окружности (мы предполагаем, что маятник не ударяется о потолок и стены). При дальнейшем падении начнёт сказываться сопротивление воздуха: ускорение лифта будет уменьшаться. Это приведёт к постепенному «включению» силы тяжести: маятник снова начнёт совершать колебания, частота которых будет увеличиваться. Через некоторое время (если высота небоскрёба достаточно велика) движение лифта станет равномерным. Если колебания маятника останутся малыми, он будет колебаться с той же частотой, что и в покоящемся лифте. 11. 12. 13. 14. 0,5 кг. 15. 790 кг/м3.
|
|
|



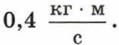
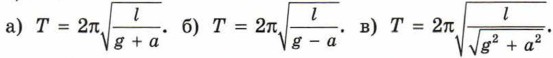 Период колебаний пружинного маятника во всех случаях одинаков:
Период колебаний пружинного маятника во всех случаях одинаков: 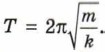 Указание. Удобно перейти в систему отсчёта, в которой точка подвеса маятника неподвижна. В этой неинерциальной системе отсчёта ускорение свободного падения отличается от обычного.
Указание. Удобно перейти в систему отсчёта, в которой точка подвеса маятника неподвижна. В этой неинерциальной системе отсчёта ускорение свободного падения отличается от обычного.
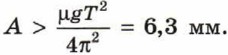 Указание. Тело покоится относительно подставки, если максимального значения силы трения покоя достаточно для сообщения телу максимального ускорения при колебаниях.
Указание. Тело покоится относительно подставки, если максимального значения силы трения покоя достаточно для сообщения телу максимального ускорения при колебаниях.
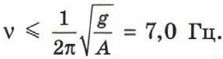 Указание. Максимальное ускорение подставки (в верхней точке) должно быть не больше ускорения свободного падения.
Указание. Максимальное ускорение подставки (в верхней точке) должно быть не больше ускорения свободного падения.
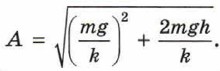 Указание. Поскольку чашка очень лёгкая, можно пренебречь потерей механической энергии при ударе шарика о чашку. Пусть максимальное отклонение чашки от начального положения равно х. Скорость чашки с шариком в этот момент равна нулю, значит, потерянная шариком потенциальная энергия mg(h + x) полностью перешла в энергию деформированной пружины
Указание. Поскольку чашка очень лёгкая, можно пренебречь потерей механической энергии при ударе шарика о чашку. Пусть максимальное отклонение чашки от начального положения равно х. Скорость чашки с шариком в этот момент равна нулю, значит, потерянная шариком потенциальная энергия mg(h + x) полностью перешла в энергию деформированной пружины 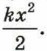 Отсюда получаем два решения:
Отсюда получаем два решения: 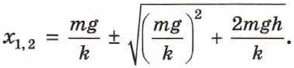 Оба решения имеют смысл и соответствуют верхнему и нижнему крайним положениям чашки при колебаниях. Среднее арифметическое двух решений, равное mg/k, соответствует положению равновесия чашки с шариком. Амплитуда А колебаний определяется из условия
Оба решения имеют смысл и соответствуют верхнему и нижнему крайним положениям чашки при колебаниях. Среднее арифметическое двух решений, равное mg/k, соответствует положению равновесия чашки с шариком. Амплитуда А колебаний определяется из условия