Общие сведения о системах счисления

Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов свидетельствуют о том, что первоначально число предметов отображали равным количеством каких-либо значков (бирок): зарубок, чёрточек, точек. Такая система записи чисел называется единичной (унарной), т. к. любое число в ней образуется путём повторения одного знака, символизирующего единицу.

Подумайте, где в наши дни можно найти отголоски унарной системы счисления.

Унарная система — не самый удобный способ записи чисел: записывать таким способом большие значения утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные и экономичные системы счисления.

Система счисления или нумерация — это способ записи (обозначения) чисел.

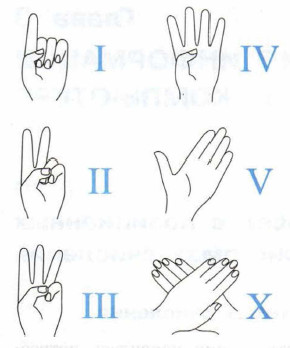
Система счисления — это знаковая система, в которой числа записываются по определённым правилам с помощью символов некоторого алфавита, называемых цифрами. Количество цифр, составляющих алфавит, называется его размерностью или мощностью.

Различают непозиционные и позиционные системы счисления.

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе.

Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две скрещённые ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (centum — сто, demimille — половина тысячи, mille — тысяча).

непозиционные системы счисления.

Чтобы записать число, римляне разлагали его на сумму тысяч (М), полутысяч (D), сотен (С), полусотен (L), десятков (X), пятёрок (V), единиц (I). Например, десятичное число 128 представляется следующим образом:

CXXVIII = 100 + 10+10 + 5 + 1 + 1 + 1
(одна сотня, два десятка, пять, три единицы).

Для записи промежуточных чисел римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. Например, XI обозначает 11, а IX обозначает 9.

Римскими цифрами пользовались очень долго. Ещё 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется в основном для наименования знаменательных дат, томов, разделов и глав в книгах.

Подумайте, почему римскую систему счисления нельзя считать полностью непозиционной.

Непозиционные системы счисления имеют ряд существенных недостатков:

существует постоянная потребность введения новых знаков для записи больших чисел;
невозможно представлять дробные и отрицательные числа;
сложно выполнять арифметические операции, т. к. не существует алгоритмов их выполнения.

Всех перечисленных недостатков лишены позиционные системы счисления.

Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа.

Например, используемая повсеместно десятичная система счисления — позиционная. Рассмотрим число 555. Цифра 5, стоящая в записи этого числа на первом месте, обозначает количество сотен и соответствует числу 500; цифра, стоящая посередине, обозначает 5 десятков (50); последняя цифра 5 соответствует пяти единицам. Исходное число можно представить в виде суммы:

555 = 500 + 50 + 5.

Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне, а завершили дело индийские математики в V-VII веках нашей эры. Важным достижением индийской науки было введение особого обозначения для пропуска разрядов — нуля. Арабы, познакомившись с этой нумерацией первыми, по достоинству её оценили, усвоили и перенесли в Европу. Получив название арабской, эта система в XII веке нашей эры распространилась по всей Европе. И так как эта система счисления проще и удобнее остальных, быстро их вытеснила.

Французский математик Пьер Симон Лаплас (1749-1827) оценил «открытие» позиционной системы такими словами: «Мысль выражать все числа немногими знаками, придавая им кроме значения по форме ещё значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна».