|
|
|
|
|
§ 10. Представление чисел в позиционных системах счисления
Позиционные системы счисленияСуществует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q > 1, называемым основанием системы счисления. Основание определяет (даёт) название системы счисления: двоичная, троичная, восьмеричная, шестнадцатеричная, q-ичная и т. д. Можно говорить «система счисления с основанием q» (табл. 3.1).
Основное достоинство любой позиционной системы счисления — возможность записи произвольного числа ограниченным количеством символов. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр: 0, 1, 2, ..., q - 1. В q-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда. Целое число без знака А в q-ичной системе счисления представляется в виде конечной суммы степеней числа q — суммы разрядных слагаемых:
Здесь:
Последовательность чисел, каждое из которых задаёт «вес» соответствующего разряда, называется базисом позиционной системы счисления.
Свёрнутой формой записи числа мы пользуемся в повседневной жизни, иначе её называют естественной формой или цифровой. Развёрнутая форма записи чисел также всем хорошо известна. Ещё в начальной школе дети учатся записывать числа в виде суммы разрядных слагаемых. Например: 125 248 = 1 • 100 000 + 2 • 10 000 + 5 • 1 000 + 2 • 100 + 4 • 10 + 8 • 1. Если представить разряды в виде степей основания, то получим: 125 248 = 1 • 105 + 2 • 104 + 5 • 103 + 2 • 102 + 4 • 101 + 8 • 100. Аналогичным образом представляются и дроби:
Иногда бывает полезно преобразовать развёрнутую форму записи числа так, чтобы избежать возведения основания системы счисления в степени. Например, можно записать: 125 248 = 1 • 105 + 2 • 104 + 5 • 103 + 2 • 102 + 4 • 101 + 8 • 100 =
0,125 = 1 • 10-1 + 2 • 10-2 + 5 • 10-3 = ((5/10 + 2)/10 + 1)/10. Такую форму представления числа называют разложением по схеме Горнера.
Но так ли хороша десятичная система счисления? Великий французский математик и естествоиспытатель Блез Паскаль (1623-1662) писал: «Десятичная система построена довольно неразумно, конечно, в соответствии с людскими обычаями, а вовсе не с требованиями естественной необходимости, как склонно думать большинство людей». В ряде теоретических и практических задач некоторые системы счисления, отличные от десятичной, имеют определённые преимущества. Первые механические счётные машины были разработаны на основе десятичной системы счисления. Для реализации десяти устойчивых состояний в них использовались сложные системы зубчатых колёс (рис. 3.1). Такие машины были очень громоздки, занимали много места.
Так, если бы проект Аналитической машины Ч. Беббиджа — механического прототипа появившихся спустя столетие ЭВМ — был реализован, то по размерам такая машина сравнялась бы с локомотивом. В 1937 году немецкий инженер К. Цузе создал вычислительную машину, основанную на принципах действия аналитической машины Ч. Беббиджа. Она была механической, но работала на основе двоичной системы счисления, что позволило значительно уменьшить её размеры: машина занимала всего 2 м2 на столе в квартире изобретателя! В наши дни большой практический интерес представляют двоичная, троичная, восьмеричная и шестнадцатеричная системы счисления.
|
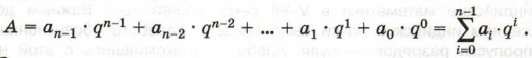
Число А, свёрнутая запись которого в системе счисления с основанием q имеет вид аn-1аn-2...а0,а-1...а-m, может быть представлено в развёрнутой форме как an-1 • qn-1 + аn-2 • qn-2 + ... + а0 • q0 + а-1 • q-1 + ... + а-m • q-m.
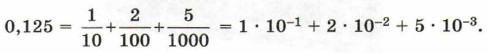
Изучая десятичную систему счисления с раннего возраста и используя её в повседневной практике, многие люди не догадываются о существовании других систем счисления.
|
|